
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��A������Ϊ����8��0����ֱ��BC������B����8��6����C��0��6�������ı���OABC�Ƶ�O��˳ʱ�뷽����ת�ǶȦ��õ��ı���OA��B��C�䣬��ʱ��OA�����BC���ڵ�P����B��C����BC���ӳ��߽��ڵ�Q������AP��
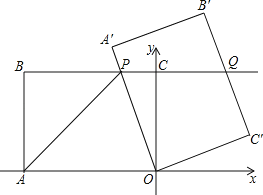
��1���ı���OABC����״�� ��
��2������ת�����У�����PAO=��POA����P�����꣮
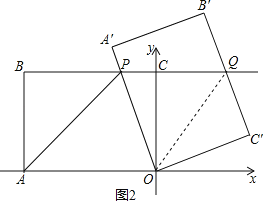
��3������ת�����У���PΪ�߶�BQ�е�ʱ������OQ������OPQ�������
���𰸡���1�����Σ���2��P����4��6������3��![]()
��������
�����������1������A��B��C������ó���COA=��OAB=��B=90���������ó��𰸣�
��2��������PAO=��POA�ó�PA=PO�������ó�AE=EO=4�����ɵó�P�����ꣻ
��3�����ȵó�Rt��OCQ��Rt��OC'Q��HL������������ƽ���ߵ����������POQ=��PQO�����ɵó�BP=PO�������ù��ɶ����ó�PQ�ij������������OPQ�������
�⣺��1������A������Ϊ����8��0������B����8��6����C��0��6����
���COA=��OAB=��B=90����
���ı���OABC�Ǿ��Σ�
�ʴ�Ϊ�����Σ�
��2����ͼ1������P��PE��AO�ڵ�E��
�ߡ�PAO=��POA��
��PA=PO��
��PE��AO��
��AE=EO=4��
��P����4��6����
��3����ͼ2����Rt��OCQ��Rt��OC'Q�У�
![]() ��
��
��Rt��OCQ��Rt��OC'Q��HL����
���OQC=��OQC'��
����OP��C'Q��
�ߡ�POQ=��OQC'��
���POQ=��PQO��
��PO=PQ��
��BP=QP��
��BP=OP=x��
��Rt��OPC��x2=��8��x��2+62��
��ã�x=![]() ��
��
��S��OPQ=![]() ��CO��PQ=
��CO��PQ=![]() ��6��
��6��![]() =
=![]() ��
��
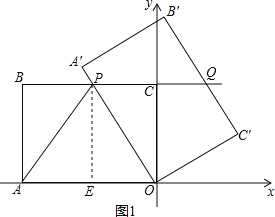



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������OAB�У���AOB=90�㣬������CDEF�Ķ���C�ǻ�AB���е㣬��D��OB�ϣ���E��OB���ӳ����ϣ���������CDEF�ı߳�Ϊ2����ͼ����Ӱ���ֵ����Ϊ�� �� 
A.�Щ�2
B.2�Щ�2
C.4�Щ�4
D.4�Щ�8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽�ͬѧ��ÿ���㻨Ǯ�����УС������������˱�У����ͬѧ�����ݵ����������Ƴ������������в�������ͳ��ͼ����
������ͳ�Ʊ�
��� | ���飨��λ��Ԫ�� | ���� |
A | 0��x��30 | 4 |
B | 30��x��60 | 16 |
C | 60��x��90 | a |
D | 90��x��120 | b |
E | x��120 | 2 |
���������ͼ��������������⣺
��1����գ���α������ͬѧ����__�ˣ�a+b=__��m=___��
��2��������ͳ��ͼ������C��Բ�ĽǶ�����
��3����У����ѧ��1000�ˣ������ÿ���㻨Ǯ������x��60��x��120��Χ��������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ƽ��ֱ������ϵ�У�![]() ��������������ֱ���
��������������ֱ���![]() ��
��![]() ��
��![]() ������
������![]() ����C����x��ĶԳƵ�Ϊ
����C����x��ĶԳƵ�Ϊ![]() ��
��![]() �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�
![]() ��ֵ����______��
��ֵ����______��![]() ��ֱ��д��
��ֱ��д��![]()
![]() �ѵ�A��ֱ��
�ѵ�A��ֱ��![]() ���ۣ����ڵ�
���ۣ����ڵ�![]() ��λ�ã������D�ڵ�һ���ޣ�
��λ�ã������D�ڵ�һ���ޣ�![]() ����
����![]() Ϊ���ĵ���ֱ�������Σ���ô��D������Ϊ______��
Ϊ���ĵ���ֱ�������Σ���ô��D������Ϊ______��![]() ��ֱ��д��
��ֱ��д��![]()
![]() ���ı���
���ı���![]() �������
�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1���������֣�
��ͼ���ھ���ABCD�У�E��BC���е㣬����ABE��AE�۵���õ���AFE����F�ھ���ABCD�ڲ����ӳ�AF��CD�ڵ�G�������߶�GF��GC�к�������ϵ����֤����Ľ��ۣ�

��2�����̽����
��ͼ������1���еľ���ABCD��Ϊƽ���ı��Σ������������䣬��1���еĽ����Ƿ���Ȼ��������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У���A����B����C�Ķ�Ӧ�߷ֱ���a��b��c����������������������ֱ�������ε��ǣ� ��
A. ��A=��B-��C B. ��A����B����C=1��3��4 C. a��b��c=1��![]() ��3 D.
��3 D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�������н��ۣ���a+b+c��0����a��b+c��0����b+2a��0����abc��0��������ȷ���������ţ� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2017��5��14����15�գ���һ��һ·�����ʺ����߷���̳�ڱ������У�������̳�ڼ䣬�й�ͬ30�������ǩ��ó����Э�飬˳�����������̰���������������ͷ��ҵ�� ��һ��һ·�����߹��Һ͵���������������ҪΪ��Щ��ҵ����һ���������ϣ���ϵ�˼ס���������ƹ�˾����˾�����ÿ�ݲ����շ�20Ԫ��������Ʒ�3000Ԫ���ҹ�˾�����ÿ�ݲ����շ�30Ԫ��������Ʒ�.������������ȫ��ͬ������£������̸�����ѡ���ļ乫˾�ȽϺ��㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ��Ŵ���ѧ����ˬ�������ɷ�Բͼ�������ĸ�ȫ�ȵ�ֱ�����������м��һ��С������ƴ�ɵ�һ���������Σ���ͼ��ʾ��������������ε������25��С�����ε������1��ֱ�������ε���ֱ�DZ߷ֱ���a��b����ô��a+b��2��ֵΪ�� ��

A��49 B��25 C��13 D��1
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com