练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．一元二次方程（k-2）x2+kx+2=0（k≠2）的根的情况是（　　）
    A．该方程有两个不相等的实数根B．该方程有两个相等的实数根
    C．该方程有实数根D．该方程没有实数根

    分析 根据方程的系数结合根的判别式，即可得出△=（k-4）2≥0，由此即可得出该方程有实数根，此题得解．

    解答 解：在方程（k-2）x2+kx+2=0中，△=k2-4×2（k-2）=k2-8k+16=（k-4）2≥0，
    ∴该方程有实数根．
    故选C．

    点评 本题考查了根的判别式，牢记“当△≥0时，方程有实数根”是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

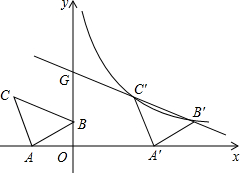    3．如图，在平面直角坐标系中有Rt△ABC，∠A=90°，AB=AC，A（-2，0），B（0，1）．
    （1）求点C的坐标；
    （2）将△ABC沿x轴的正方向平移，在第一象限内B、C两点的对应点B'、C'正好落在某反比例函数图象上．请求出这个反比例函数和此时的直线B'C'的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．有下列3个不同的问题情境：
    ①某登山队大本营所在地的气温为5℃，海拔每升高1km气温下降6℃．登山队员由大本营向上登高x km时，他们所在位置的气温是y℃；
    ②正方形边长为3，若边长增加x，则面积增加y；
    ③某种活期储蓄的月利率是0.06%，存入100元本金，则本息和（本金与利息的和）y随所存月数x变化；
    若用函数解析式表示y与x的关系，那么符合一次函数关系的问题情境的个数为（　　）
    A．0B．1C．2D．3

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．下列因式分解正确的是（　　）
    A．x2-y2=（x-y）2B．a2+a+1=（a+1）2
    C．2xy-6x=2x（y-3）D．a2+4a+21=a（a+4）+21

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．在实数3，-3，-$\sqrt{3}$，$\sqrt{3}$中最小的数是（　　）
    A．3B．-3C．$\sqrt{3}$D．-$\sqrt{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．如图1，已知二次函数y=ax2+bx+c（a、b、c为常数，a≠0）的图象过点O（0，0）和点A（4，0），函数图象最低点M的纵坐标为-$\frac{8}{3}$，直线l的解析式为y=x．

    （1）求二次函数的解析式；
    （2）直线l沿x轴向右平移，得直线l′，l′与线段OA相交于点B，与x轴下方的抛物线相交于点C，过点C作CE⊥x轴于点E，把△BCE沿直线l′折叠，当点E恰好落在抛物线上点E′时（图2），求直线l′的解析式；
    （3）在（2）的条件下，l′与y轴交于点N，把△BON绕点O逆时针旋转135°得到△B′ON′，P为l′上的动点，当△PB′N′为等腰三角形时，求符合条件的点P的坐标．

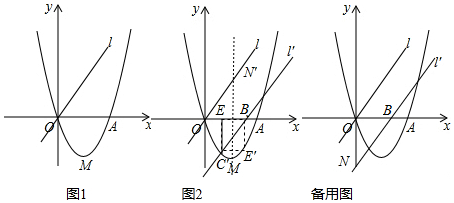
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

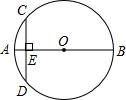    5．如图，AB是⊙O的直径，弦CD⊥AB于点E．若AB=8，AE=1，则弦CD的长是（　　）
    A．$\sqrt{7}$B．2$\sqrt{7}$C．6D．8

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

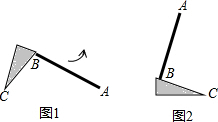    2．如图1，教室里有一只倒地的装垃圾的灰斗，BC与地面的夹角为50°，∠C=25°，小贤同学将它绕点C旋转一定角度，扶起平放在地面上（如图2），则灰斗柄AB绕点C转动的角度为（　　）
    A．75°B．25°C．115°D．105°

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．据报道，2016年单位就业人员年平均工资超过70300元，将数70300用科学记数法表示为7.03×104．

    查看答案和解析>>

    同步练习册答案