
【题目】如图,AB为⊙O的直径,射线AP交⊙O于C点,∠PCO的平分线交⊙O于D点,过点D作![]() 交AP于E点.
交AP于E点.
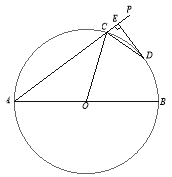
(1)求证:DE为⊙O的切线;
(2)若DE=3,AC=8,求直径AB的长.
【答案】(1)证明见解析;(2)10.
【解析】
试题(1)连接OD若要证明DE为⊙O的切线,只要证明∠DOE=90°即可;
(2)过点O作OF⊥AP于F,利用垂径定理以及勾股定理计算即可.
试题解析:连接OD.

∵OC=OD,
∴∠1=∠3.
∵CD平分∠PCO,
∴∠1=∠2.
∴∠2=∠3.
∵DE⊥AP,
∴∠2+∠EDC=90°.
∴∠3+∠EDC=90°.
即∠ODE=90°.
∴OD⊥DE.
∴DE为⊙O的切线.
(2)过点O作OF⊥AP于F.
由垂径定理得,AF=CF.
∵AC=8,
∴AF=4.
∵OD⊥DE,DE⊥AP,
∴四边形ODEF为矩形.
∴OF=DE.
∵DE=3,
∴OF=3.
在Rt△AOF中,OA2=OF2+AF2=42+32=25.
∴OA=5.
∴AB=2OA=10.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某中学为推动“时刻听党话 永远跟党走”校园主题教育活动,计划开展四项活动:A:党史演讲比赛,B:党史手抄报比赛,C:党史知识竞赛,D:红色歌咏比赛.校团委对学生最喜欢的一项活动进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2两幅不完整的统计图.请结合图中信息解答下列问题:
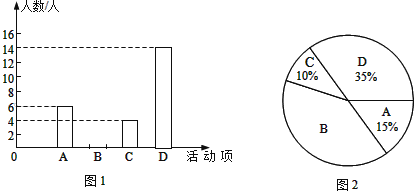
(1)本次共调查了 名学生;
(2)将图1的统计图补充完整;
(3)已知在被调查的最喜欢“党史知识竞赛”项目的4个学生中只有1名女生,现从这4名学生中任意抽取2名学生参加该项目比赛,请用画树状图或列表的方法,求出恰好抽到一名男生一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
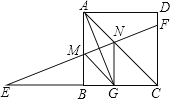
【题目】如图,在正方形ABCD中,∠BAC的平分线交BC边于G,AG的中垂线与CB的延长线交于E,与AB、AC、DC分别交于点M,N,F,下列结论:①tan∠E=![]() ,②△AGC≌△EMG,③四边形AMGN是菱形,④S△CFN=S四边形AMGN,其中正确的是______(填序号).
,②△AGC≌△EMG,③四边形AMGN是菱形,④S△CFN=S四边形AMGN,其中正确的是______(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边三角形ABC在平面直角坐标系中的位置如图所示,C(1,0),点A在y轴的正半轴上,把等边三角形ABC沿x轴正半轴作无滑动的连续翻转,每次翻转120°,经过2018次翻转之后,点C的坐标是______.
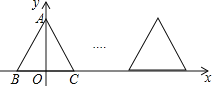
查看答案和解析>>
科目:初中数学 来源: 题型:
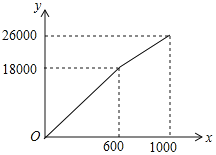
【题目】为了创建“全国文明城市”,鄂州市积极主动建设美丽家园,某社区拟将一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草面积为x(m2),种草费用y1(元)与x(m2)的函数关系式为y1=![]() ,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系如表所示:
,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系如表所示:
x(m2) | 100 | 200 | 300 |
y2(元) | 3900 | 7600 | 11100 |
(1)请直接写出y1与种草面积x(m2)的函数关系式,y2与栽花面积x(m2)的函数关系式;
(2)设这块1000m2空地的绿化总费用为W(元),请利用W与种草面积x(m2)的函数关系式,求出绿化总费用W的最大值;
(3)若种草部分的面积不少于600m2,栽花部分的面积不少于200m2,请求出绿化总费用W的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知方程![]() ,
,
(1)求证:方程一定有两个不相等的实数根;
(2)![]() 取何值时,方程二根中一个比3大,一个比3小。(可用数形结合来解)
取何值时,方程二根中一个比3大,一个比3小。(可用数形结合来解)
(3)![]() 取何值时方程的两个根异号且负的实数根的绝对值大.
取何值时方程的两个根异号且负的实数根的绝对值大.
查看答案和解析>>
科目:初中数学 来源: 题型:
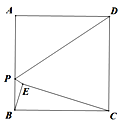
【题目】如图,正方形ABCD的边长为6,点E是正方形内部一点,连接BE,CE,且∠ABE=∠BCE,点P是边AB上一动点,连接PD,PE,则PD+PE的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,半径BO与AC相交于点D,BO的延长线与⊙O交于点F,与过点C的切线NC交于点M,过点D作DE⊥BC,垂足为E,连接CF,已知MF=FC.
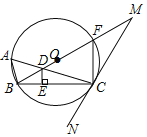
(1)求证:∠M=30°;
(2)①若![]() =
=![]() ,求
,求![]() 的值;
的值;
②当△DEC的面积是它最大值的![]() 时,求
时,求![]() 的值.
的值.
(3)若DE=![]() AB,试判断点D所在的位置.(请直接写出答案)
AB,试判断点D所在的位置.(请直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
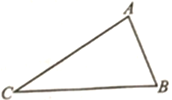
【题目】如图,△ABC中,AC=8,BC=10,AC>AB.
(1)用尺规作图法在△ABC内求作一点D,使点D到两点A、C的距离相等,又到边AC、BC的距离相等(保留作图痕迹,不写作法).
(2)若△ACD的周长为18,求△BCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com