
【题目】如图,四边形ABCD各顶点的坐标分别为(-2,8),(-11,6),(-14,0),(0,0).
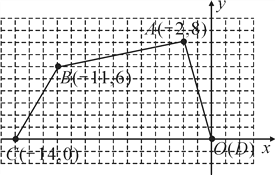
(1)确定这个四边形的面积,你是怎样做的?
(2)如果把四边形ABCD各顶点纵坐标保持不变,横坐标增加2,所得的四边形面积又是多少?
【答案】(1) 80;(2)80
解:(1) (1)S四边形ABCD=14×8-![]() ×8×2-2×3-
×8×2-2×3-![]() ×2×9-
×2×9-![]() ×3×6=112-8-6-9-9=80 (2)各顶点纵坐标保持不变,横坐标增加2,即把四边形ABCD向右平移2个单位,所以形状、大小不发生改变,面积也不变,仍是80
×3×6=112-8-6-9-9=80 (2)各顶点纵坐标保持不变,横坐标增加2,即把四边形ABCD向右平移2个单位,所以形状、大小不发生改变,面积也不变,仍是80
【解析】试题分析:(1)过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,把四边形ABCD的面积分成两个三角形的面积与梯形的面积的和,然后列式求解即可;
(2)横坐标增加2,纵坐标不变,就是把四边形ABCD向右平移2个单位,根据平移的性质,四边形的面积不变.
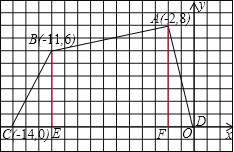
试题解析:(1)如图,过点A作AF⊥x轴,过点B作BE⊥x轴,
则DF=2,CE=3,AF=8,BE=6,EF=-2-(-11)=9,
四边形ABCD的面积=S△ADF+S△BCE+S梯形ABEF,
=![]() ×2×8+
×2×8+![]() ×3×6+
×3×6+![]() ×(6+8)×9,
×(6+8)×9,
=8+9+63,
=80;
(2)四边形ABCD各个顶点的纵坐标保持不变,横坐标增加4,
就是把四边形ABCD向右平移4个单位,
所以,所得的四边形的面积不变,还是80.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
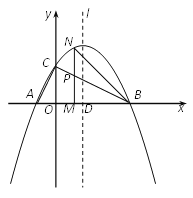
【题目】如图,已知抛物线![]() (其中
(其中![]() )与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,抛物线的对称轴l与x轴交于点D,且点D恰好在线段BC的垂直平分线上.
)与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,抛物线的对称轴l与x轴交于点D,且点D恰好在线段BC的垂直平分线上.
(1)求抛物线的关系式;
(2)过点![]() 的线段MN∥y轴,与BC交于点P,与抛物线交于点N.若点E是直线l上一点,且∠BED=∠MNB-∠ACO时,求点E的坐标.
的线段MN∥y轴,与BC交于点P,与抛物线交于点N.若点E是直线l上一点,且∠BED=∠MNB-∠ACO时,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用的时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示,下列说法错误的是( )

A.小明中途休息用了20分钟
B.小明休息前爬山的平均速度为每分钟70米
C.小明在上述过程中所走的路程为6600米
D.小明休息前爬山的平均速度大于休息后爬山的平均速度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用反证法证明命题“在三角形中,至多有一个内角是直角”时,应先假设( )
A. 至少有一个内角是直角 B. 至少有两个内角是直角
C. 至多有一个内角是直角 D. 至多有两个内角是直角
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,D(0,﹣3),M(4,﹣3),直角三角形ABC的边与x轴分别交于O、G两点,与直线DM分别交于E、F点. 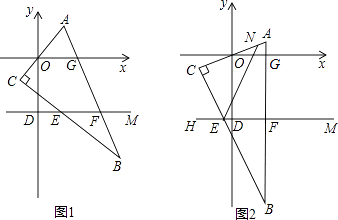
(1)将直角三角形ABC如图1位置摆放,请写出∠CEF与∠AOG之间的等量关系: .
(2)将直角三角形ABC如图2位置摆放,N为AC上一点,∠NED+∠CEF=180°,请写出∠NEF与∠AOG之间的等量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学学生志愿服务小组在“学雷锋”活动中,购买了一批牛奶到敬老院慰问老人.如果送给每位老人2盒牛奶,那么剩下16盒;如果送给每位老人3盒牛奶,那么正好送完.则敬老院有_____位老人.
查看答案和解析>>
科目:初中数学 来源: 题型:
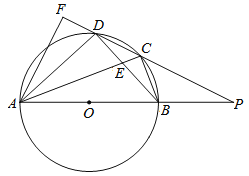
【题目】如图,四边形ABCD内接于⊙O,AB是⊙O的直径,AC和BD相交于点E,且DC2=CECA.
(1)求证:BC=CD;
(2)分别延长AB,DC交于点P,过点A作AF⊥CD交CD的延长线于点F,若PB=OB,CD=![]() ,求DF的长.
,求DF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com