
| A. | y1≤y2 | B. | y1<y2 | C. | y1≥y2 | D. | y1>y2 |
科目:初中数学 来源: 题型:解答题
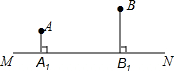 如图,直线MN表示一条铁路,A,B是两个城市,它们到铁路的垂直距离分别为AA1=20km,BB1=40km,已知A1B1=80km,现要在A1,B1之间设一个中转站P,使两个城市到中转站的距离之和最短,请你设计一种方案确定P点的位置,并求这个最短距离.
如图,直线MN表示一条铁路,A,B是两个城市,它们到铁路的垂直距离分别为AA1=20km,BB1=40km,已知A1B1=80km,现要在A1,B1之间设一个中转站P,使两个城市到中转站的距离之和最短,请你设计一种方案确定P点的位置,并求这个最短距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
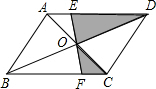 如图,?ABCD的面积是8,对角线AC、DB交于点O,EF过点O分别交AD、BC于E、F,则阴影部分的面积是( )
如图,?ABCD的面积是8,对角线AC、DB交于点O,EF过点O分别交AD、BC于E、F,则阴影部分的面积是( )| A. | 4 | B. | 2 | C. | 6 | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com