
 (1)计算:|-2+$\sqrt{3}$|+(-1)2017-(π+1)0+$\sqrt{3}$;
(1)计算:|-2+$\sqrt{3}$|+(-1)2017-(π+1)0+$\sqrt{3}$;分析 (1)根据绝对值、特殊角的三角函数值、零指数幂、负整数指数幂可以解答本题;
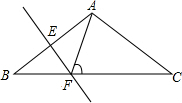
(2)先由等腰三角形的性质求出∠B的度数,再由垂直平分线的性质可得出∠BAF=∠B,由三角形内角与外角的关系即可解答.
解答 解:(1)|-2+$\sqrt{3}$|+(-1)2017-(π+1)0+$\sqrt{3}$
=2-$\sqrt{3}$-1-1+$\sqrt{3}$=0;
(2)∵AB=AC,∠BAC=120°,
∴∠B=(180°-120°)÷2=30°,
∵EF垂直平分AB,
∴BF=AF,
∴∠BAF=∠B=30°,
∴∠AFC=∠BAF+∠B=60°.
点评 本题考查的是绝对值、特殊角的三角函数值、零指数幂、负整数指数幂、线段垂直平分线的性质,即线段的垂直平分线上的点到线段的两个端点的距离相等.


科目:初中数学 来源: 题型:解答题
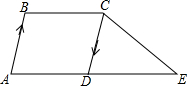 如图,在?ABCD中,点E在边AD的延长线上,DE=AD,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$.
如图,在?ABCD中,点E在边AD的延长线上,DE=AD,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 3元,3.5元 | B. | 3.5元,3元 | C. | 4元,4.5元 | D. | 4.5元,4元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
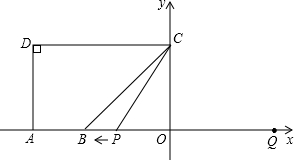 如图,已知A(-5,0)、B(-3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB,∠CDA=90°点,P从点Q(4,0)出发,沿x轴向左以每秒1个单位长度的速度运动,运动时间ts.
如图,已知A(-5,0)、B(-3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB,∠CDA=90°点,P从点Q(4,0)出发,沿x轴向左以每秒1个单位长度的速度运动,运动时间ts.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com