【题目】某天，一蔬菜经营户用60元钱从蔬菜批发市场批了西红柿和豆角共40㎏到菜市场去卖，西红柿和豆角这天的批发价与零售价如下表所示：问：他当天卖完这些西红柿和豆角能赚多少钱？
品名 | 西红柿 | 豆角 |
批发价（单位：元/kg） | 1.2 | 1.6 |
零售价（单位：元/kg） | 1.8 | 2.5 |
开心蛙口算题卡系列答案科目：初中数学 来源： 题型：
【题目】如图，A，B两地被池塘隔开，小明通过下列方法测出了A，B间的距离：先在AB外选一点C，然后测出AC，BC的中点M，N，并测量出MN的长为12 m，由此他就知道了A，B间的距离，有关他这次探究活动的描述错误的是( )
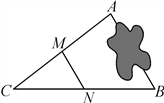
A. AB=24 m B. MN∥AB C. △CMN∽△CAB D. CM∶MA=1∶2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①，平面直角坐标系XOY中，若A（0，a）、B（b，0）且（a﹣4）2+
=0，以AB为直角边作等腰Rt△ABC，∠CAB=90°，AB=AC．
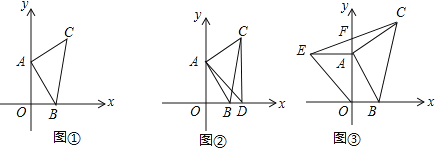
（1）求C点坐标；
（2）如图②过C点作CD⊥X轴于D，连接AD，求∠ADC的度数；
（3）如图③在（1）中，点A在Y轴上运动，以OA为直角边作等腰Rt△OAE，连接EC，交Y轴于F，试问A点在运动过程中S△AOB：S△AEF的值是否会发生变化？如果没有变化，请直接写出它们的比值 （不需要解答过程或说明理由）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】王老师家买了一套新房，其结构如图所示(单位：m)．他打算将卧室铺上木地板，其余部分铺上地砖．
(1)木地板和地砖分别需要多少平方米？
(2)如果地砖的价格为每平方米x元，木地板的价格为每平方米3x元，那么王老师需要花多少钱？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在学习了全等三角形和等边三角形的知识后，张老师出了如下一道题：如图，点B是线段AC上任意一点，分别以AB、BC为边在AC同一侧作等边△ABD和等边△BCE，连接CD、AE分别与BE和DB交于点N、M，连接MN．求证：△ABE≌△DBC．
接着张老师又让学生分小组进行探究：你还能得出什么结论？
精英小组探究的结论是：AM=DN
奋斗小组探究的结论是：△EMB≌△CNB．
创新小组探究的结论是：MN∥AC．
（1）你认为哪一小组探究的结论是正确的？
（2）选择其中你认为正确的一种情形加以证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在RtΔABC中，∠C=90，AC=4cm，BC=3cm．动点M、N从点C同时出发，均以每秒1cm的速度分别沿CA、CB向终点A、B移动，同时动点P从点B出发，以每秒2cm的速度沿BA向终点A移动。连接PM、PN。设移动时间为t（单位：秒，0<t<2．5）．
（1）当t为何值时，以A、P、M为顶点的三角形与ΔABC相似？
（2）是否存在某一时刻t，使△PMN 的面积恰好是△ABC 面积的
；若存在求t的值；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，AD平分∠BAC，
(1)图①中，已知AF⊥BC , ∠B=500，∠C=600. 求∠DAF的度数.
（2）图②中，请你在直线AD上任意取一点E（不与点A、D重合），画EF⊥BC，垂足为F.已知∠B=α，∠C=β（β＞a）.求∠DEF的度数. （用α、β的代数式表示）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察下列方程及解的特征： ⑴x+
=2的解为x1=x2=1；
⑵x+
=
的解为x1=2，x2=
；
⑶x+
=
的解为x1=3，x2=
；
解答下列问题：
（1）请猜想：方程x+
=
的解为________；
（2）请猜想：关于x的方程x+
═________的解为x1=a，x2=
（a≠0）；
（3）下面以解方程x+
=
为例，验证（1）中猜想结论的正确性．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
