
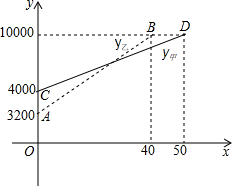
 2016年国庆期间,某校准备组织部分教职工到黄山风景区旅游.经市场调研发现.如图,线段CD表示甲旅行社所需总费用y甲(元)与旅游人数x的函数图象,线段AB表示乙旅行社所需总费用y乙(元)与旅游人数x的函数图象,根据图象提供的信息,解答下列问题:
2016年国庆期间,某校准备组织部分教职工到黄山风景区旅游.经市场调研发现.如图,线段CD表示甲旅行社所需总费用y甲(元)与旅游人数x的函数图象,线段AB表示乙旅行社所需总费用y乙(元)与旅游人数x的函数图象,根据图象提供的信息,解答下列问题:分析 (1)根据待定系数法,可得函数解析式;
(2)根据函数与不等式的关系,可得答案;
(3)根据函数与不等式的关系,可得答案.
解答 解:(1)设甲的解析式为y=kx+b,将(0,4000)(50,10000)代入函数解析式,得
$\left\{\begin{array}{l}{b=4000}\\{50k+b=10000}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=120}\\{b=4000}\end{array}\right.$,
y甲=120x+4000;
设乙的解析式为y=cx+d,将(0,3200)(40,10000)代入函数解析式,得
$\left\{\begin{array}{l}{d=3200}\\{40c+d=10000}\end{array}\right.$,
解得$\left\{\begin{array}{l}{c=170}\\{d=3200}\end{array}\right.$,
y乙=170x+3200;
(2)当y甲=y乙时,120x+4000=170x+3200,
解得x=16,
当0≤x<16时,选择乙合算;
当x=16时,甲与乙都一样;
当16<x<50时,选择甲合算;
(3)当x=10时,选择乙旅行社费用少,费用是1700+3200=20200元;
当x=16时,甲乙旅行社都可以,费用是120×16+4000=5920元;
当x=30时,选择甲旅行社费用少,120×30+4000=7600元.
点评 本题考查了一次函数的应用,利用待定系数法是解(1)的题关键;利用函数与不等式的关系是解(2)(3)的题关键;


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 车型 | 甲 | 乙 | 丙 |
| 汽车运载量(吨/辆) | 5 | 8 | 10 |
| 汽车运费(元/辆) | 400 | 500 | 600 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 购票人数 | 1~50人 | 51~100人 | 100人以上 |
| 每人门票价 | 13元 | 11元 | 9元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
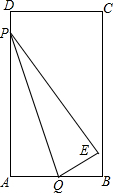 如图,矩形纸ABCD,AB=3,AD=6,动点Q从点A出发以每秒1个单位长的速度沿AB向终点B运动,运动$\frac{2}{3}$秒时,动点P从点D出发以相等的速度沿DA向终点A运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).将△APQ沿PQ翻折,得到△EPQ
如图,矩形纸ABCD,AB=3,AD=6,动点Q从点A出发以每秒1个单位长的速度沿AB向终点B运动,运动$\frac{2}{3}$秒时,动点P从点D出发以相等的速度沿DA向终点A运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).将△APQ沿PQ翻折,得到△EPQ查看答案和解析>>
科目:初中数学 来源: 题型:解答题
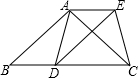 已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.
已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
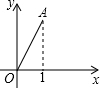 如图,在平面直角坐标系中,点A(1,$\sqrt{3}$),若将点A绕点O顺时针旋转150°得到点B,则点B的坐标为( )
如图,在平面直角坐标系中,点A(1,$\sqrt{3}$),若将点A绕点O顺时针旋转150°得到点B,则点B的坐标为( )| A. | (0,2) | B. | (0,-2) | C. | (-1,-$\sqrt{3}$) | D. | ($\sqrt{3}$,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com