列方程解应用题:
(1)2010年春季我国西南五省持续干旱,旱情牵动着全国人民的心.“一方有难、八方支援”,某厂计划生产1800吨纯净水支援灾区人民,为忙把纯净水发往灾区,工人把每天的工作效率提高到原计划的1.5倍,结果比原计划提前3天完成了生产任务,求原计划每天生产多少吨纯净水?
(2)某校八年级两个班各为玉树地震灾区捐款1800元.已知2班比1班人均捐款多4元,2班的人数比1班的人数少10%.请你根据上述信息,就这两个班级的“人数”或“人均捐款”提出一个用分式方程解决的问题,并写出解题过程.
解:(1)设原计划每天生产x吨纯净水,则

-3=

x=200.
经检验x=200是分式方程的解.
原计划生产200吨水.
(2)设1班有x人,则
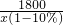
-

=4
x=50.
经检验x=50是分式方程的解.
50×(1-10%)=45.
1班有50人,2班有45人.
分析:(1)设原计划每天生产x吨纯净水,根据某厂计划生产1800吨纯净水支援灾区人民,为忙把纯净水发往灾区,工人把每天的工作效率提高到原计划的1.5倍,结果比原计划提前3天完成了生产任务,可列方程求解.
(2)求两个班的人数,设1班有x人,根据两个班各为玉树地震灾区捐款1800元.已知2班比1班人均捐款多4元,2班的人数比1班的人数少10%,根据此可列方程求解.
点评:本题考查理解题意的能力,第一题设出计划的以时间做为等量关系列方程求解,第二题设出人数,以人均捐款数的差做为等量关系列方程求解.

 -3=
-3=
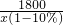 -
- =4
=4

 目标测试系列答案
目标测试系列答案