
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:选择题
| A. | y=2x+1 | B. | y=$\frac{2}{{x}^{2}}$ | C. | y=$\frac{3}{x}$ | D. | 2y=x |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
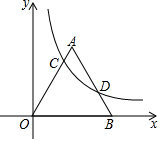 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与边长为5的等边△AOB的边OA,AB分别相交于C,D两点,若OC=2BD,则实数k的值为( )
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与边长为5的等边△AOB的边OA,AB分别相交于C,D两点,若OC=2BD,则实数k的值为( )| A. | $4\sqrt{3}$ | B. | $\frac{25}{4}\sqrt{3}$ | C. | $\frac{9}{2}\sqrt{3}$ | D. | $8\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
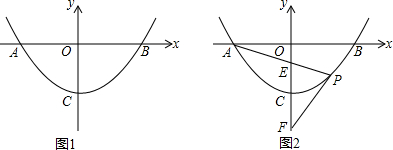
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了解甲、乙两名运动员的体能训练情况,对他们进行了跟踪测试,并把连续十周的测试成绩绘制成如图所示的折线统计图.教练组规定:体能体能测试成绩70分以上(包括70分)为合适.
为了解甲、乙两名运动员的体能训练情况,对他们进行了跟踪测试,并把连续十周的测试成绩绘制成如图所示的折线统计图.教练组规定:体能体能测试成绩70分以上(包括70分)为合适.| 平均数 | 中位数 | 体能测试成绩合格次数 | |
| 甲 | 60 | 65 | 2 |
| 乙 | 60 | 57.5 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 13 | B. | 14 | C. | 12 | D. | 11 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
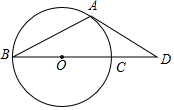 如图,已知BC是⊙O的直径,AB是⊙O的弦,切线AD交BC的延长线于D,若∠D=40°,则∠B的度数是( )
如图,已知BC是⊙O的直径,AB是⊙O的弦,切线AD交BC的延长线于D,若∠D=40°,则∠B的度数是( )| A. | 40° | B. | 50° | C. | 25° | D. | 115° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com