
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���![]() ��
��![]() ���������ϣ���
���������ϣ���![]() ��
��![]() ��������������
��������������![]()
![]() �ij�Ϊ
�ij�Ϊ![]() ������
������![]() �Dz���ʽ
�Dz���ʽ![]() �����������
�����������
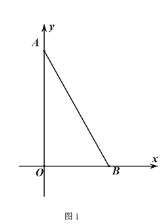
��1����![]() �ij�
�ij�
��2������![]() ��ÿ��
��ÿ��![]() ����λ���ȵ��ٶ���
����λ���ȵ��ٶ���![]() �ϴ�
�ϴ�![]() ����
����![]() ���˶�����
���˶�����![]() �ij���Ϊ
�ij���Ϊ![]() �˶�ʱ��Ϊ
�˶�ʱ��Ϊ![]() �����ú�
�����ú�![]() ��ʽ�ӱ�ʾ
��ʽ�ӱ�ʾ![]() ��
��
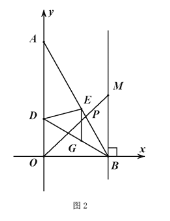
��3����ͼ2���ڣ�2�����������£�![]() ƽ��
ƽ��![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() ��
��![]() �ϣ���
�ϣ���![]() ��
��![]() �ϣ�����
�ϣ�����![]() ����
����![]() ����
����![]() ���
���![]() ��������IJ�Ϊ
��������IJ�Ϊ![]() ������
������![]() �����ӳ�����
�����ӳ�����![]() ������
������![]() �ᴹֱ��ֱ����
�ᴹֱ��ֱ����![]() ����
����![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ������
������![]() ��ֵ��
��ֵ��
���𰸡���1��10��2��d��102t��0��t��5����3��t=3��![]() =3
=3
��������
��1���Ƚⲻ��ʽ![]() �ã�a��11������ȷ����a�����ɵó����ۣ�
�ã�a��11������ȷ����a�����ɵó����ۣ�
��2�����˶�֪AP��2t�����ɵó����ۣ�
��3�����жϳ���DEN�ա�DEG��SAS�����ó���BND����DGE����EDN����EDB��45![]() ��������BDN��90
��������BDN��90![]() ������ͬ�ǣ���Ƚǣ����������жϳ���DGE����BDO���ó�EG��OD���������EG��2������S��OBP��S��BPM��3��2���ó�
������ͬ�ǣ���Ƚǣ����������жϳ���DGE����BDO���ó�EG��OD���������EG��2������S��OBP��S��BPM��3��2���ó�![]() �������ó�
�������ó�![]() ����
����![]() �����AP��6�����ɵó����ۣ�
�����AP��6�����ɵó����ۣ�
��1���ⲻ��ʽ����ʽ![]() �ã�a��11��
�ã�a��11��
��a�Dz���ʽ![]() ����������⣬
����������⣬
��a��10��
��AB�ij�Ϊa��
��AB�ij�Ϊ10��
��2���ɣ�1��֪��AB��10��
���˶�֪��AP��2t��
��d=BP��ABAP��102t��0��t��5����
��3����ͼ2����EA�Ͻ�ȡEN��EG��
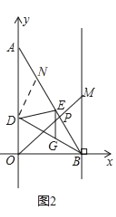
�ߡ�AED����GED��DE��DE��
���DEN�ա�DEG��SAS����
���BND����DGE����EDN����EDB��45![]() ��
��
���BDN����EDB����EDN��90![]() ��
��
���BND����DBN��90![]() ��
��
���DGE����DBN��90![]() ��
��
��BDƽ�֡�ABO��y���ڵ�D��
���DBN����DBO��
���DGE����DBO��90![]() ��
��
�ߡ�BDO����DBO��90![]() ��
��
���DGE����BDO��
��EG��OD��
�ߵ�E���G��������IJ�Ϊ2��
��EG��2��
��S��OBP��S��BPM��3��2��
��S��OBM��S��BPM��5��2��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��AP��6��
��t��6��2��3�룬![]() =
=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʵ���Ƚϴ�С��ȷ���ǣ� ��
A.3��|��7|
B.![]() ��3
��3 ![]()
C.0����2
D.�� ![]() ��2��3��1
��2��3��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=BC��BE��AC�ڵ�E��AD��BC�ڵ�D����BAD=45�㣬AD��BE���ڵ�F������CF��
��1����֤��BF=2AE��
��2����CD=![]() ����AD�ij���
����AD�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC������Ϊ1�ĵ���ֱ�����Σ���Rt��ABC��б��ACΪֱ�DZߣ����ڶ�������Rt��ACD������Rt��ACD��б��ADΪֱ�DZߣ�������������Rt��ADE�������������ƣ����2018������ֱ�������ε�б�߳���______��
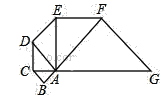
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������
��ͼ��EF��AD,��1=��2,��BAC=70��.�����AGD�Ĺ�����д����.
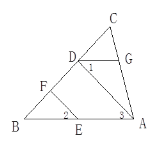
�⣺ ��ΪEF��AD��
���ԡ�2=____ (_________________________________)
������1=��2
���ԡ�1=��3 (__________________)
����AB��_____ (___________________________________)
���ԡ�BAC+______=180��(___________________________)
����BAC=70��
���ԡ�AGD=_______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
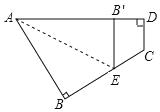
����Ŀ����ͼ��ʾ��һ���ı���ֽƬ ABCD����B=��D=90������ֽƬ����ͼ��ʾ�۵���ʹ�� B ���� AD ���ϵ� B���㣬AE ���ۺۣ�
(1)���ж� B��E �� DC ��λ�ù�ϵ����˵�����ɣ�
(2)�����C=128�������AEB �Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�AB��EG��x�ᣬBC��DE��HG��AP��y�ᣬ��D��C��P��H��x���ϣ�A(1��2)��B(��1��2)��D(��3��0)��E(��3����2)��G(3����2)����һ����Ϊ2018����λ������û�е��Ե�ϸ���ߵĴ�ϸ���Բ���)��һ�˹̶��ڵ�A��������A��B��C��D��E��F��G��H����P��A���Ĺ��ɽ�����ͼ�Ρ����ı��ϣ���ϸ����һ������λ�õĵ��������(����)
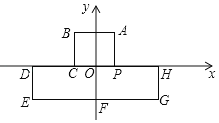
A. (1��2)B. (��1��2)C. (��1��0)D. (1��0)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ⷽ�̣�
��1��x2+3x-4=0�� ��2����x+1��2=4x��
��3��x��x+4��=-5��x+4���� ��4��2x2-4x-1=0.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ����ٽ���
�ⷽ�̣�x��1��2��5��x��1��+4=0�����Խ���x��1������һ�����壬��x��1=y����ԭ���̿ɻ�y2��5y+4=0�����y1=1��y2=4����y=1ʱ����x��1=1�����x=2����y=4ʱ����x��1=4�����x=5���� ԭ���̵Ľ�Ϊx1=2��x2=5
�������������ַ����ⷽ�̣���3x��5��2��4��5��3x��+3=0��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com