
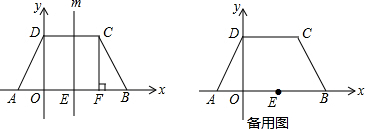
���� ��1�����ݶԳ���д��B��C��������ꣻ
��2����ΪC��D�ǶԳƵ㣬��������BD��ֱ��m�Ľ����������ĵ�M����ʱ��MBC���ܳ���̣��ֱ����ù��ɶ������BD��BC�ij�����Ӽ��ɣ�
��3�������ı���ABCD�����Ϊ9����Ϊֱ��m�Ƶ�E��ת360�㣬��ijһ�����ε�һ��ΪAE��BE����AE=BE=2����Ϊ�ֳ����Ϊ1��5�������֣���S��ADE��S��BCEΪ3�����Ը�ֱ����ֱ��DE��ֱ��CE���·�����������ɷֱ������Ӧ�ĸ�FG=$\frac{3}{2}$��Ҫ��������ֱ����ֱ��m�Ľ���ʽ��
���  �⣺��1�����ı���ABCD�ĶԳ����ǣ�ֱ��m=1��
�⣺��1�����ı���ABCD�ĶԳ����ǣ�ֱ��m=1��
�ɶԳƵã�B��3��0����C��2��3����
�ʴ�Ϊ����3��0������2��3����
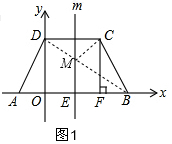
��2������BD��ֱ��m��M������CM����ʱ��MBC���ܳ���̣�
��m�ǶԳ��ᣬ
��m���߶�CD���д��ߣ�
��DM=CM��
��CM+BM=DM+BM��
��Rt��DOB����OD=3��OB=3��
��BD=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$��
��CM+BM=BD=3$\sqrt{2}$��
��C��CF��x����F��
��C��2��3����B��3��0����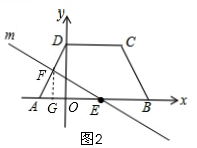
��BF=3-2=1��CF=3��
�ɹ��ɶ����ã�BC=$\sqrt{B{F}^{2}+C{F}^{2}}$=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$��
���BMC���ܳ�=CM+BM+BC=3$\sqrt{2}$+$\sqrt{10}$��
��3��������ã��ı���ABCDΪ����
��S�ı���ABCD=$\frac{1}{2}$��DC+AB����OD=$\frac{1}{2}$����2+4����3=9
����ת������m���ı���ABCD�ֳ����Ϊ1��5�������֣�
�����������
����ͼ2��S��AFE��S�����EFDCB=1��5��
��F��FG��AB��G��
��S��AFE=$\frac{1}{2}$��2��FG=9��$\frac{1}{6}$��
��FG=$\frac{3}{2}$��
��FG��OD��
���AFG�ס�ADO��
��$\frac{FG}{OD}=\frac{AG}{AO}$��
��$\frac{\frac{3}{2}}{3}=\frac{AG}{1}$��
��AG=$\frac{1}{2}$��
��OG=$\frac{1}{2}$��
��F��-$\frac{1}{2}$��$\frac{3}{2}$����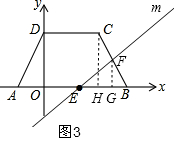
��ֱ��m�Ľ���ʽΪ��y=kx+b��
��F��-$\frac{1}{2}$��$\frac{3}{2}$����E��1��0������ã�$\left\{\begin{array}{l}{-\frac{1}{2}k+b=\frac{3}{2}}\\{k+b=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-1}\\{b=1}\end{array}\right.$��
��ֱ��m�Ľ���ʽΪ��y=-x+1��
����ͼ3��S�����AEFCD��S��BEF=5��1��
��F��FG��AB��G����C��CH��AB��H����FG��CH��
ͬ������ã�FG=$\frac{3}{2}$��BG=$\frac{1}{2}$��
��OG=OB-BG=3-$\frac{1}{2}$=$\frac{5}{2}$��
��F��$\frac{5}{2}$��$\frac{3}{2}$����
��ֱ��m�Ľ���ʽΪ��y=kx+b��
��F��$\frac{5}{2}$��$\frac{3}{2}$����E��1��0������ã�$\left\{\begin{array}{l}{\frac{5}{2}k+b=\frac{3}{2}}\\{k+b=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=1}\\{b=-1}\end{array}\right.$��
��ֱ��m�Ľ���ʽΪ��y=x-1��
������������ʱֱ��m�ĺ�������ʽΪy=-x+1��y=x-1��
���� �������ı��ε��ۺ��⣬���������Ρ���Գơ����������ε����ʺ��ж����Լ����·�����⣬��ȷ�Գ����ǶԳƵ����ߵ��д��ߣ������������������Ƶ��ж������ʣ��뺯�����ϣ����ô���ϵ������һ�κ����Ľ���ʽ����3���ѶȽϴ������˷������۵�˼�룬ע��ֳ����Ϊ1��5�������֣��������ν�ϵ�˼���������⣮


 ֥�鿪���γ�������ϵ�д�
֥�鿪���γ�������ϵ�д� ����ѧ��ţ��Ӣ��ϵ�д�
����ѧ��ţ��Ӣ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -8 | B�� | 8 | C�� | $\frac{1}{8}$ | D�� | -$\frac{1}{8}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
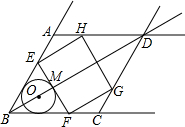 ��ͼ��������BA��BC��AD��CDΧ�ɵ�����ABCD�У���ABC=60�㣬AB=6$\sqrt{3}$��O������BD��һ�㣬��O��BA��BC�����С���BO���ӳ��߽��ڵ�M����M��EF��BD���߶�BA�����߶�AD���ڵ�E�����߶�BC�����߶�CD���ڵ�F����EFΪ��������EFGH����G��H�ֱ���Χ�����ε����������߶��ϣ�
��ͼ��������BA��BC��AD��CDΧ�ɵ�����ABCD�У���ABC=60�㣬AB=6$\sqrt{3}$��O������BD��һ�㣬��O��BA��BC�����С���BO���ӳ��߽��ڵ�M����M��EF��BD���߶�BA�����߶�AD���ڵ�E�����߶�BC�����߶�CD���ڵ�F����EFΪ��������EFGH����G��H�ֱ���Χ�����ε����������߶��ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
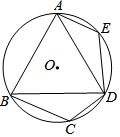 ��ͼ���ڡ�O���ڽ��ı���ABCD�У�AB=AD��E�ڻ�AD��һ�㣮
��ͼ���ڡ�O���ڽ��ı���ABCD�У�AB=AD��E�ڻ�AD��һ�㣮�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com