练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．下列图形中既是轴对称图形又是中心对称图形的是（　　）
    A．
    等边三角形    		B．
    平行四边形    		C．
    正五边形    		D．
    圆

    分析 根据中心对称图形与轴对称图形的概念进行判断即可．

    解答 解：等边三角形是轴对称图形不是中心对称图形；
    平行四边形不是轴对称图形是中心对称图形；
    正五边形是轴对称图形不是中心对称图形；
    圆是轴对称图形又是中心对称图形，
    故选：D．

    点评 本题考查的是中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    9．如图，正方形ABCD中，AB=6，点E在边CD上，且CD=3DE，将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG、CF，下列结论：
    ①△ABG≌△AFG；②BG=GC；③AG∥CF；④S△FGC=$\frac{18}{5}$．
    其中正确结论的个数是（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

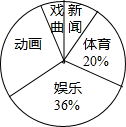    10．为了解某地区七年级学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况，从该地区随机抽取部分七年级学生作为样本，采用问卷调查的方法收集数据（参与问卷调查的每名同学只能选择其中一类节目），并调查得到的数据用下面的表和扇形图来表示（表、图都没制作完成）
    节目类型新闻体育动画娱乐戏曲
    人数3690ab27
    根据表、图提供的信息，解决以下问题：
    （1）计算出表中a、b的值；
    （2）求扇形统计图中表示“动画”部分所对应的扇形的圆心角度数；
    （3）若该地区七年级学生共有47500人，试估计该地区七年级学生中喜爱“新闻”类电视节目的学生有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

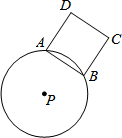    7．如图，⊙P的半径为5，A、B是圆上任意两点，且AB=6，以AB为边作正方形ABCD（点D、P在直线AB两侧）．若AB边绕点P旋转一周，则CD边扫过的面积为9π．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．抛物线y=x2+bx+c（其中b，c是常数）过点A（2，6），且抛物线的对称轴与线段y=0（1≤x≤3）有交点，则c的值不可能是（　　）
    A．4B．6C．8D．10

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．某校为了解全校学生上学期参加社区活动的情况，学校随机调查了本校50名学生参加社区活动的次数，并将调查所得的数据整理如下：
       参加社区活动次数的频数、频率分布表
    活动次数x频数频率
    0＜x≤3100.20
    3＜x≤6a0.24
    6＜x≤9160.32
    9＜x≤1260.12
    12＜x≤15mb
    15＜x≤182n
    根据以上图表信息，解答下列问题：
    （1）表中a=12，b=0.08；
    （2）请把频数分布直方图补充完整（画图后请标注相应的数据）；
    （3）若该校共有1200名学生，请估计该校在上学期参加社区活动超过6次的学生有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．已知M=$\frac{2}{9}$a-1，N=a2-$\frac{7}{9}$a（a为任意实数），则M、N的大小关系为（　　）
    A．M＜NB．M=NC．M＞ND．不能确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．如图是由6个棱长均为1的正方体组成的几何体，它的主视图的面积为5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

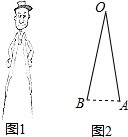    9．如图1是一副创意卡通圆规，图2是其平面示意图，OA是支撑臂，OB是旋转臂，使用时，以点A为支撑点，铅笔芯端点B可绕点A旋转作出圆．已知OA=OB=10cm．
    （1）当∠AOB=18°时，求所作圆的半径；（结果精确到0.01cm）
    （2）保持∠AOB=18°不变，在旋转臂OB末端的铅笔芯折断了一截的情况下，作出的圆与（1）中所作圆的大小相等，求铅笔芯折断部分的长度．（结果精确到0.01cm）
    （参考数据：sin9°≈0.1564，cos9°≈0.9877，sin18°≈0.3090，cos18°≈0.9511，可使用科学计算器）

    查看答案和解析>>

    同步练习册答案