Question

9．如图，在平面直角坐标系中，直线l_AB：y=-$\frac{3}{4}$x+$\frac{15}{2}$与x轴交于点B，且与过原点的直线l_OA互相垂直且交于点A（$\frac{18}{5}$，m），正方形CDEF的其中一个顶点C与原点重合，另一顶点E在反比例函数y=-$\frac{16}{x}$上，正方形CDEF从现在位置出发，在射线OB上以每秒1个单位长度的速度向右平移，运动时间为t．
（1）当D落在线段AO上时t=3，当D落在线段AB上时t=$\frac{14}{3}$．
（2）记△ABO与正方形CDEF重叠面积为S，当0≤t≤7时，请直接写出S与t的函数关系式以及t的取值范围．
（3）在正方形CDEF从图1位置开始向右移动的同时，另一动点P在线段AB上以每秒1个单位长度的速度从B点运动到A点，当0≤t≤8时，请求出使得△CAP是以AC为腰的等腰三角形的t的值．

Answer 1

分析 （1）先求点A的坐标，并求直线l_OA的解析式；根据正方形CDEF的一点E在反比例函数y=-$\frac{16}{x}$上，则边长为4，平移得，点D的纵坐标总是4，横坐标为其速度t，因此点D在哪条直线上，就代入哪个解析式即可；
（2）分三种情况讨论：①当0≤t≤3时，如图2，重叠面积为△OCG的面积，利用面积公式求得；②当3＜t≤$\frac{14}{3}$时，如图3，过G作GM⊥x轴于M，重叠面积为正方形CDEF面积减去△EGH的面积；③当$\frac{14}{3}$＜t≤7，如图4，重叠面积S=16-S_△EGH-S_△DMN；
（3）如图5，先求点P的坐标，分两种情况：如图6，当AC=AP时，根据图形构建两个直角三角形，利用勾股定理列方程解出t的值；如图7，当AC=PC时，同理可得t的值．

解答 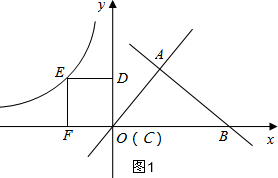解：（1）当x=$\frac{18}{5}$时，y=-$\frac{3}{4}$×$\frac{18}{5}$+$\frac{15}{2}$=$\frac{24}{5}$，
∴A（$\frac{18}{5}$，$\frac{24}{5}$），
设l_OA的解析式为：y=kx，
把A（$\frac{18}{5}$，$\frac{24}{5}$）代入得：$\frac{24}{5}$=$\frac{18}{5}$k，
k=$\frac{4}{3}$，
∴l_OA的解析式为：y=$\frac{4}{3}$x，
由正方形CDEF的一点E在反比例函数y=-$\frac{16}{x}$上，
则正方形边长为4，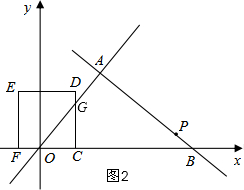
设D（t，4），
当D落在线段AO上时，4=$\frac{4}{3}$t，t=3，
当D落在线段AB上时，4=-$\frac{3}{4}$t+$\frac{15}{2}$，t=$\frac{14}{3}$，
故答案为：3，$\frac{14}{3}$；
（2）①当0≤t≤3时，如图2，
∵OC=t，则CG=$\frac{4}{3}$t，
∴S=$\frac{1}{2}$CG•OC=$\frac{1}{2}$×t×$\frac{4}{3}$t=$\frac{2}{3}$t²，
②当3＜t≤$\frac{14}{3}$时，如图3，过G作GM⊥x轴于M，则tan∠GOM=$\frac{4}{3}$，OF=t-4，
∴tan∠GOM=$\frac{FH}{OF}$，
∴FH=$\frac{4}{3}$（t-4），
∴EH=4-$\frac{4}{3}$（t-4），
∵EG=FM=3-（t-4）=7-t，
∴S=16-S_△EGH=16-$\frac{1}{2}$×EH×EG=16-$\frac{1}{2}$[4-$\frac{4}{3}$（t-4）]（7-t）=-$\frac{2}{3}$t²+$\frac{28}{3}$t-$\frac{50}{3}$；
③当$\frac{14}{3}$＜t≤7，如图4，
当y=0，-$\frac{3}{4}$x+$\frac{15}{2}$=0，x=10，
∵HM=$\frac{14}{3}$-3=$\frac{2}{3}$，DM=OC-OQ=t-$\frac{14}{3}$，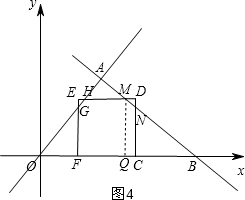
过M作MQ⊥x轴于Q，则MQ=4，OQ=$\frac{14}{3}$，BQ=10-$\frac{14}{3}$=$\frac{16}{3}$，
∴tan∠MBQ=$\frac{MQ}{BQ}$=$\frac{4}{\frac{16}{3}}$=$\frac{3}{4}$，
∵ED∥FC，
∴∠DMN=∠MBQ，
∴tan∠DMN=$\frac{3}{4}$，
∴$\frac{ND}{MD}$=$\frac{3}{4}$，
∴ND=$\frac{3}{4}$（t-$\frac{14}{3}$），
∴S=16-S_△EGH-S_△DMN，
=-$\frac{2}{3}$t²+$\frac{28}{3}$t-$\frac{50}{3}$-$\frac{1}{2}$（t-$\frac{14}{3}$）$•\frac{3}{4}（t-\frac{14}{3}）$，
=-$\frac{25}{24}{t}^{2}$+$\frac{77}{6}$t-$\frac{149}{6}$；
（3）如图5，过P作PQ⊥x轴于Q，
由（2）得：tan∠PBQ=$\frac{3}{4}$，
∵BP=t，
∴PQ=$\frac{3t}{5}$，BQ=$\frac{4t}{5}$，
∴OQ=OB-BQ=10-$\frac{4t}{5}$，
∴P（10-$\frac{4t}{5}$，$\frac{3t}{5}$），
如图6，当AC=AP时，过A作AG⊥x轴于G，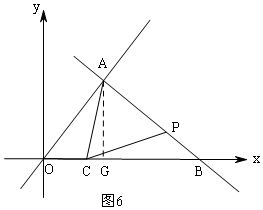
∵OB=10，OG=$\frac{18}{5}$，
∴GB=10-$\frac{18}{5}$=$\frac{32}{5}$，
由勾股定理得：AB=$\sqrt{（\frac{24}{5}）^{2}+（\frac{32}{5}）^{2}}$=8，
∴AP=AC=8-t，CG=$\frac{18}{5}$-t，

在Rt△ACG中，得$\sqrt{（\frac{18}{5}-t）^{2}+（\frac{24}{5}）^{2}}$=AC²=AP²=（8-t）²，

解得：t=$\frac{35}{11}$，
如图7，当AC=PC时，同理构建Rt△ACG和Rt△PCQ，
得：$\sqrt{（\frac{18}{5}-t）^{2}+（\frac{24}{5}）^{2}}$=$\sqrt{（\frac{3t}{5}）+（10-\frac{4t}{5}-t）^{2}}$，
解得：t₁=8（舍）或t₂=$\frac{40}{13}$，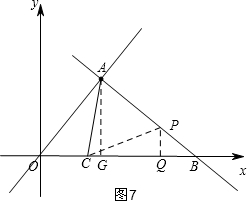
综上所述：使得△CAP是以AC为腰的等腰三角形的t的值为$\frac{35}{11}$或$\frac{40}{13}$．

点评 本题是反比例函数的综合题，考查了利用待定系数法求反比例函数和一次函数的解析式；对于求两图形重叠部分的面积，要先确定其特殊位置时t的值，弄清运动过程中形成的重叠部分图形的形状分几类，从而确定分几种情况进行讨论；再求t的值时，与方程相结合，利用勾股定理列方程．