
【题目】阅读
(1)阅读理解: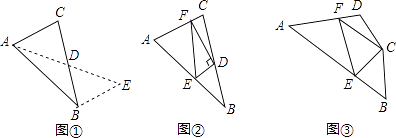
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB,AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.
中线AD的取值范围是;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以C为顶点作一个70°角,角的两边分别交AB,AD于E,F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.
【答案】
(1)2<AD<8
(2)
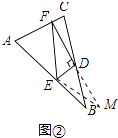
解:证明:延长FD至点M,使DM=DF,连接BM,EM,如图②所示:
同(1)得:△BMD≌△CFD(SAS),
∴BM=CF,
∵DE⊥DF,DM=DF,
∴EM=EF,
在△BME中,由三角形的三边关系得:BE+BM>EM,
∴BE+CF>EF
(3)
解:BE+DF=EF;理由如下:
延长AB至点N,使BN=DF,连接CN,如图3所示:
∵∠ABC+∠D=180°,∠NBC+∠ABC=180°,
∴∠NBC=∠D,
在△NBC和△FDC中, 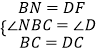 ,
,
∴△NBC≌△FDC(SAS),
∴CN=CF,∠NCB=∠FCD,
∵∠BCD=140°,∠ECF=70°,
∴∠BCE+∠FCD=70°,
∴∠ECN=70°=∠ECF,
在△NCE和△FCE中, 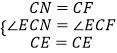 ,
,
∴△NCE≌△FCE(SAS),
∴EN=EF,
∵BE+BN=EN,
∴BE+DF=EF

【解析】(1)解:延长AD至E,使DE=AD,连接BE,如图①所示:
∵AD是BC边上的中线,
∴BD=CD,
在△BDE和△CDA中,  ,
,
∴△BDE≌△CDA(SAS),
∴BE=AC=6,
在△ABE中,由三角形的三边关系得:AB﹣BE<AE<AB+BE,
∴10﹣6<AE<10+6,即4<AE<16,
∴2<AD<8;
所以答案是:2<AD<8;
【考点精析】本题主要考查了全等三角形的性质的相关知识点,需要掌握全等三角形的对应边相等; 全等三角形的对应角相等才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y1=ax+b(a≠0)的图象与y轴相交于点A,与反比例函数y2=![]() (c≠0)的图象相交于点B(3,2)、C(﹣1,n).
(c≠0)的图象相交于点B(3,2)、C(﹣1,n).
(1)求一次函数和反比例函数的解析式;
(2)根据图象,直接写出y1>y2时x的取值范围;
(3)在y轴上是否存在点P,使△PAB为直角三角形?如果存在,请求点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABE和△ADC分别沿着边AB,AC翻折180°形成的,若∠BCA:∠ABC:∠BAC=28:5:3,BE与DC交于点F,则∠EFC的度数为( ) 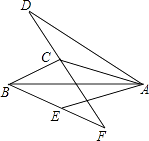
A.20°
B.30°
C.40°
D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将代数式x2+6x+2化成(x+p)2+q的形式为( )
A. (x-3)2+11 B. (x+3)2-7 C. (x+3)2-11 D. (x+2)2+4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( ) 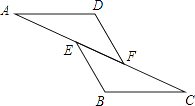
A.∠A=∠C
B.AD=CB
C.BE=DF
D.AD∥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AC⊥BC,AE为∠BAC的平分线,DE⊥AB,AB=7cm,AC=3cm,则BD等于( ) 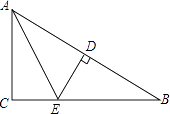
A.1cm
B.2cm
C.3cm
D.4cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC≌△DEC,∠ACB=60°,∠BCD=100°,点A恰好落在线段ED上,则∠B的度数为( ) 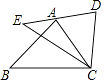
A.50°
B.60°
C.55°
D.65°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索规律
观察下列各式及验证过程:n=2时,有式①: ![]() ;n=3时,有式②:
;n=3时,有式②: ![]() ;
;
式①验证: ![]()
式②验证: ![]()
![]()
(1)针对上述式①、式②的规律,请写出n=4时的式子;
(2)请写出满足上述规律的用n(n为任意自然数,且n≥2)表示的等式,并加以验证.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com