
����Ŀ��2015��2��27�գ�������ȫ����ĸ��쵼С���ʮ�λ����ϣ�����ͨ���ˡ��й�����ĸ����巽���������Ƹĸ�����ĸУ����ȳ�Ϊ�ĸ�����㣮���������棬��Ϊ�������ˮƽ�����������й��������������Ѿ������12����ͷ���г������Ѿ�����������Ĺ�ע��ͼ9��ijһ���ֹ�����ڶ��ֱ������ӵĻ���ͳ��ͼ��

(1)����ͼ������������_____֧�г���Ӳ�����
(2)��ȫͼһ�е�����ͳ��ͼ��
(3)���������������ʤһ����3�֣�ƽһ����1�֣���һ����0�֣����÷������Ϊ�ھ��������ڶ��ֱ��������λ��ǰ4���ķֱ���A��49�֣�B��49�֣�C��48�֣�D��45�֣������һ�ֵı����У����Ƿֱ�͵�4���Ժ����ӽ��б�������֪���Ѿ�������һ�������У�A�ӺͶ��ִ�ƽ�������б�������״ͼ�ķ���������C�Ӷ�ùھ��ĸ����Ƕ��٣�
���𰸡���1��16����2������������3��![]() .
.
��������
���������б��ó�A��B��C��D�ĸ������4���Ժ����ӽ��б������е÷ֽ�����ɱ��������ֵ����������ѡ����������C�ӻ�ʤ�����������������Ӷ������C�ӻ�ʤ�ĸ��ʣ�
�⣺��1��4��25%��16��֧����
�𣺸�����16֧�г���Ӳ�����
�ʴ�Ϊ��16��
��2������Ϊ39.5��44.5�����Ϊ16��1��3��6��4��2��֧����
��ȫ����ͳ��ͼ��ͼ��ʾ��
��3�����������

�ɱ���õ���������27�ֱ������ֽ����
��50��52��51��48������50��52��51��46������50��52��51��45����
��50��52��49��48������50��52��49��46������50��52��49��45����
��50��52��48��48������50��52��48��46������50��52��48��45����
��50��50��51��48������50��50��51��46������50��50��51��45����
��50��50��49��48������50��50��49��46������50��50��49��45����
��50��50��48��48������50��50��48��46������50��50��48��45����
��50��49��51��48������50��49��51��46������50��49��51��45����
��50��49��49��48������50��49��49��46������50��49��49��45����
��50��49��48��48������50��49��48��46������50��49��48��45����
������֪A�Ӵ�ƽ��C�ӻ�ʤ�����ǡ��6�֣�
��P��C�ӻ�ʤ��![]()




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������������ÿ̨���۷ֱ�Ϊ2000Ԫ��1700Ԫ��A��B�����ͺŵĿյ�������ǽ����ܵ����������
����ʱ�� | �������� | �������� | |
A���ͺ� | B���ͺ� | ||
��һ�� | 3̨ | 5̨ | 18000Ԫ |
�ڶ��� | 4̨ | 10̨ | 31000Ԫ |
�����ۡ��ۼ۾����ֲ��䣬������������������ɱ���
��1����A��B�����ͺŵĿյ������۵��ۣ�
��2�����������ò�����54000Ԫ�Ľ���ٲɹ��������ͺŵĿյ���30̨����A���ͺŵĿյ�����ܲɹ�����̨��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ACB=90�㣬O��AB��һ�㣬��OAΪ�뾶�ġ�O��BC�����ڵ�D����AB���ڵ�E������ED���ӳ���AC���ӳ����ڵ�F��
��1����֤��AE=AF��
��2����DE=3��sin��BDE=![]() ����AC�ij���
����AC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
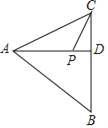
����Ŀ����ͼ���ڡ�ABC�У�AD�Ǹߣ�BD��6��CD��4��tan��BAD��![]() ��P���߶�AD��һ���㣬һ�����˴ӵ�A������AD��
��P���߶�AD��һ���㣬һ�����˴ӵ�A������AD��![]() ����λ/����ٶ��ߵ�P�㣬Ȼ����1����λ/����ٶ���PC�ߵ�C�㣬������t�룬��t����СֵΪ_____��
����λ/����ٶ��ߵ�P�㣬Ȼ����1����λ/����ٶ���PC�ߵ�C�㣬������t�룬��t����СֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�������y����![]() x2+2
x2+2![]() x��
x��![]() ��x�ύ��A��B����(��A�ڵ�B�����)����y�ύ�ڵ�C������ΪD���Գ�����x�ύ�ڵ�E��ֱ��CE���������ڵ�F(���ڵ�C)��ֱ��CD��x�ύ�ڵ�G��
��x�ύ��A��B����(��A�ڵ�B�����)����y�ύ�ڵ�C������ΪD���Գ�����x�ύ�ڵ�E��ֱ��CE���������ڵ�F(���ڵ�C)��ֱ��CD��x�ύ�ڵ�G��
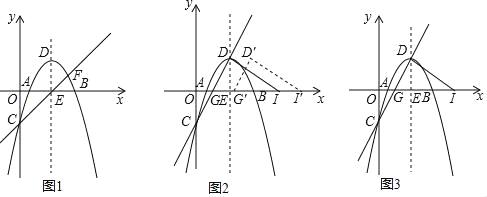
(1)��ͼ1����ֱ��CE�Ľ���ʽ�Ͷ���D�����ꣻ
(2)��ͼ1����PΪֱ��CF�Ϸ���������һ�㣬����PC��PF������PCF��������ʱ����M�ǹ�P��ֱ��x���ֱ��l��һ�㣬��N�������߶Գ�����һ�㣬��FM+MN+NO����Сֵ��
(3)��ͼ2������D��DI��DG��x���ڵ�I������GDI������GB����ƽ������G��D��I����������G��D��I���Ƶ�D����ʱ����ת��(0������180��)������ת��һ������ʱ����G�������I�غϣ�����ת�����еġ�G��D��I��Ϊ��G��D��I��������������ת�����У�ֱ��G��I���ֱ�x���ֱ��GD���ڵ�K��L���㣬�Ƿ����������K��L��ʹ��GKLΪ�ԡ�LGKΪ�ǵĵ��������Σ������ڣ����ʱGL�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
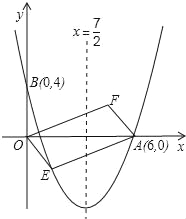
����Ŀ����ͼ���Գ���Ϊֱ��x��![]() �������߾�����A(6��0)��B(0��4)��
�������߾�����A(6��0)��B(0��4)��
(1)�������߱���ʽ���������ꣻ
(2)���E(x��y)����������һ���㣬��λ�ڵ������ޣ��ı���OEAF����OAΪ�Խ��ߵ�ƽ���ı��Σ���ƽ���ı���OEAF�����S��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
(3)��(2)�����£��Ƿ���ڵ�E��ʹƽ���ı���OEAFΪ�����Σ������ڣ������E�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
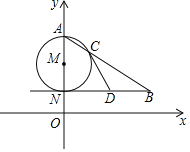
����Ŀ����ͼ��AN����M��ֱ����NB��x�ᣬAB����M�ڵ�C��
��1������A��0��6����N��0��2������ABN=30�㣬���B�����ꣻ
��2����DΪ�߶�NB���е㣬��֤��ֱ��CD����M�����ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�������y��mx2��2mx+m+4��y�ύ�ڵ�A��0��3������x�ύ�ڵ�B��C����B�ڵ�C��ࣩ��
��1����������ߵı���ʽ����B��C�����ꣻ
��2�������ߵĶԳ�����x�ύ�ڵ�D����ֱ��y��kx+b������D�͵�E����1����2������ֱ��DE�ı���ʽ��
��3���ڣ�2���������£���֪��P��t��0��������P����ֱ��x���ֱ�߽��������ڵ�M����ֱ��DE�ڵ�N������M�͵�N��������һ������x���·���ֱ��д��t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�![]() �Ķ��㶼�������Σ�ÿ��С�����α߳�Ϊ��λ1������ĸ���ϣ�
�Ķ��㶼�������Σ�ÿ��С�����α߳�Ϊ��λ1������ĸ���ϣ�
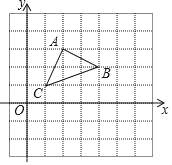
��1��![]() ����״���� ����ֱ��д�𰸣�
����״���� ����ֱ��д�𰸣�
��2������![]() ��
��![]() �ᷭ�ۺ��
�ᷭ�ۺ��![]() ��
��
��3������![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת
˳ʱ����ת![]() ��
��![]() �������ת������
�������ת������![]() ɨ������������������
ɨ������������������![]() ��
��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com