练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．一个三角形改变成和它相似的三角形，
    （1）若边长扩大为原来的4倍，则面积扩大为原来的16倍．
    （2）若面积扩大为原来的4倍，则周长扩大为原来的2倍．

    分析 （1）根据相似三角形的面积比等于相似比的平方得出即可；
    （2）根据相似三角形的面积比等于相似比的平方，相似三角形的周长比等于相似比得出即可．

    解答 解：（1）∵一个三角形改变成和它相似的三角形，
    ∴边长扩大为原来的4倍，则面积扩大为原来16倍，
    故答案为：16；

    （2）∵一个三角形改变成和它相似的三角形，
    ∴若面积扩大为原来的4倍，则周长扩大为原来的2倍，
    故答案为2．

    点评 本题考查了相似三角形的性质的应用，能正确运用相似三角形的性质进行计算是解此题的关键，注意：相似三角形的面积比等于相似比的平方，相似三角形的周长比等于相似比．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    10．作图与计算：在所给图中仅用直尺和圆规按要求作图（保留作图痕迹，不写作法）
    （1）作Rt△ABC的外接圆，圆心为O；
    （2）以AB为对称轴，作点C的对称点为C′，CC′交AB于E；
    （3）当BC=1，AC=2时，计算Rt△ABC绕直线AB旋转一周形成的几何体的侧面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．如图，长方形ABCD的长BC为3cm，宽AB为2cm，点E、F是边AD的三等分点，点G、H是边BC的三等分点．现分别以B、G两点为圆心，以2cm长为半径画弧AH和弧EC，则阴影部分的面积为2cm2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

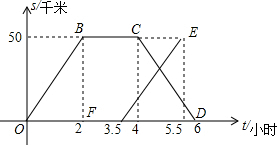    8．为搜集植物标本，老师带领第一组同学从学校先乘车出发，寻找到目的地，采集中，向另一组同学报告，采完后立即返回，第二组同学接到报告后，立即从学校出发，如图是两组同学与学校的距离s和离开学校的时间t之间的函数图象．（假设两组同学沿同一路线行进）
    （1）直接写出第一组同学离开学校的距离s和他们离开学校的时间t之间的函数关系式；
    （2）求两组同学相遇时，他们与学校的距离；
    （3）在两组同学行动的过程中，求第一组同学出发多少时间后与第二组同学相距12.5km？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．市政府决定对市区某路段进行扩建，现从甲乙两个工程队提供的资料可知，若两队合做，24天可以完工，若两队合做8天后，再由乙队独做40天也能完工，现在甲队每天的施工费用为3万元，乙队每天的施工费用为1.5万元．
    （1）甲乙两队单独施工各需要多少天完成工程？
    （2）根据工程预算，总费用不得超过114万元，而现在接到大运会组委会通知，要求该工程不超过30天完工，请你帮忙决策，至少让乙队参与施工多少天？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．如图，在菱形ABCD中，AB=BD，点E、F分别在AB、AD上，且AE=DF，连接BF与DE相交于点G，连接CG与BD相交于点H．若CG=8，则S四边形BCDG=16$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图，在梯形ABCD中，AB∥CD，∠ADC=90°，AB=6，AD=3，CD=2，在Rt△EFG中，∠GEF=90°，EF=3，GE=6，△EFG（点F和点A重合）的边EF和梯形的边AB在同一直线上．现Rt△EFG将从A以每秒1个单位的速度向射线AB方向匀速平移，当点F与点B重合时停止运动，设运动时间为t秒，解答下列问题：

    （1）求线段BC的长度；
    （2）在整个运动过程中，设△EFG与△ABD重叠部分的面积为S，请直接写出S与t的函数关系式和相应t的取值范围；
    （3）当点F到达点B时，将△EFG绕点F顺时针旋转α（0＜α＜180°），旋转过程中EF所在直线交CD所在直线于M，是否存在这样的α，使△BCM为等腰三角形？若存在，求DM的长；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．如图小明在楼上点A处测得旗杆BC顶部B的仰角为30°，测得旗杆底部C的俯角为60°，已知点A距地面高AD为12m，旗杆的高度为16 m．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．已知a2-2（k-1）ab+9b2是一个完全平方式，那么k=4或-2．

    查看答案和解析>>

    同步练习册答案