
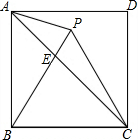
 如图,点P在正方形ABCD内,△PBC是正三角形,AC与PB相交于点B,有以下结论:
如图,点P在正方形ABCD内,△PBC是正三角形,AC与PB相交于点B,有以下结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据等边三角形性质得出∠PCB=60°,PC=BC,∠PBC=60°,根据正方形性质和等腰三角形性质求出∠DBC=45°,即可判断①;
根据三角形内角和定理和三角形外角性质求出∠DPC=∠PDC=75°,即可判断②;
根据三角形相似的判定即可判断③;
根据三角形的面积求出△PBC,△DPC,△DBC的面积,即可判断④.
解答 解:∵△BCP是等边三角形,
∴∠PCB=60°,
∵四边形ABCD是正方形,
∴∠ACB=45°,
∴∠ACP=∠BCP-∠ACB=60°-45°=15°,∴①正确;
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∵△BCP是等边三角形,
∴∠BAC=45°,BP=BC,∠PBC=60°,
∴AB=BP,
∴∠BAP=∠BPA=$\frac{1}{2}×$(180°-∠ABP)=$\frac{1}{2}$[180°-(90°-60°)]=75°,
∴∠PAE=∠BAP-∠BAC=75°-45°=30°,
∴∠AEP=180°-∠APB-∠PAE=180°-75°-30°=75°,
∴∠APE=∠AEP,
∴△APE是等腰三角形,∴②正确;
∵∠PAE=∠ABP=30°,∠APB=∠APE,
∴△APE∽△BPA,
∴$\frac{AP}{PE}$=$\frac{BP}{AP}$,
∵AP=AE,AB=BP,
∴AE2=PE•AB,∴③正确;
连接PD,过D作DG⊥PC于G,过P作PF⊥AD于F,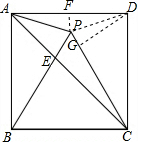
设正方形的边长为2a,则S2=4a2,等边三角形PBC的边长为2a,高为$\sqrt{3}$a,
∴PF=2a-$\sqrt{3}$a=(2-$\sqrt{3}$)a,
∴S△APD=$\frac{1}{2}$AD•PF=(2-$\sqrt{3}$)a2,
∴∠PCD=90°-60°=30°,
∴GD=$\frac{1}{2}$CD=a,
∴S△PCD=$\frac{1}{2}$PC•DG=a2,S△ACD=2a2,
∴S1=S△ACD-S△ADP-S△PCD=2a2-a2-(2-$\sqrt{3}$)a2=($\sqrt{3}$-1)a2<a2,
∴S1:S2≠1:4.
∴④错误;
故选C.
点评 本题考查了正方形性质,等边三角形的性质,含30度角的直角三角形,三角形面积,等腰三角形的性质,三角形的内角和定理,相似三角形的判定等知识点的应用,主要考查学生的推理能力,题目是一道中等题.


科目:初中数学 来源: 题型:解答题
| 序号 | 第一枪 | 第二枪 | 第三枪 | 总环数 | 方差 |
| 甲选手 | 8 | a | b | 27 | $\frac{2}{3}$ |
| 乙选手 | 8.2 | 8.8 | 9.1 | 26.1 | $\frac{7}{50}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k>$\frac{1}{2}$且k≠1 | B. | k≥$\frac{1}{2}$且k≠1 | C. | k≤-$\frac{1}{2}$ | D. | k?$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,抛物线C1:y=x2+bx+c与x轴交于点A,B(点A在点B的左侧),对称轴与x轴交于点(3,0),且AB=4.
在平面直角坐标系xOy中,抛物线C1:y=x2+bx+c与x轴交于点A,B(点A在点B的左侧),对称轴与x轴交于点(3,0),且AB=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com