Question

10．如图，在△ABC中，∠ACB=90°，AC=BC，点D在边AB上，点P在线段CD上，且AD=2DB，∠APB=135°
（1）探究线段AP和BP之间的数量关系；
（2）若AC=3，求CP的长．

Answer 1

分析 （1）结论：AP=$\sqrt{2}$PB．如图，作AP′⊥CD于P′，连接BP′，作BE⊥CD于E．理由同一法证明P与P′是同一点，即可解决问题．
（2）在Rt△ACP中，设PC=m，则AP=2m，理由勾股定理即可解决问题．

解答 解：（1）结论：AP=$\sqrt{2}$PB．
理由：如图，作AP′⊥CD于P′，连接BP′，作BE⊥CD于E．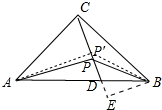

∵AP′∥BE，
∴$\frac{AD}{DB}$=$\frac{AP′}{BE}$=$\frac{1}{2}$，
∵∠ACP′+∠BCE=90°，∠BCE+∠CBE=90°，
∴∠ACP′=∠CBE，
在△ACP′和△CBE中，
$\left\{\begin{array}{l}{∠ACP′=∠CBE}\\{∠AP′C=∠E=90°}\\{AC=BC}\end{array}\right.$，
∴△ACP′≌△CBE，
∴AP′=EC=2EB，CP′=BE，
∴P′C=P′E=EB，
∴∠EP′B=∠EBP′=45°，
∴∠AP′B=∠AP′E+∠BP′E=135°，∵∠APB=135°，
∴P与P′共点，
设BE=EP=a，则AP=2a，PB=$\sqrt{2}$a，
∴AP：PB=$\sqrt{2}$：1，
∴AP=$\sqrt{2}$PB．

（2）在Rt△ACP中，设PC=m，则AP=2m，
∴AC²=PC²+AP²，
∴9=5m²，
∵m＞0，
∴m=$\frac{3\sqrt{5}}{5}$，
∴CP的长为$\frac{3\sqrt{5}}{5}$．

点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质、勾股定理等知识，解题的关键是理由同一法证明，学会添加辅助线方法，题目比较难．