
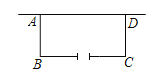
【题目】某校在基地参加社会活动中,带队老师考问学生:基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长69米的不锈钢栅栏围成,与墙平行的一边留有一个宽为3米的出入口,如图所示.如何设计才能使园地的面积![]() 最大?下面是两位同学争议的情境:小军:把它围成一个正方形,这样的面积一定最大.小英:不对啦!面积最大的不是正方形.请根据上面信息,解决问题:
最大?下面是两位同学争议的情境:小军:把它围成一个正方形,这样的面积一定最大.小英:不对啦!面积最大的不是正方形.请根据上面信息,解决问题:
(1)设![]() 米(
米(![]() ).
).
①![]() 米(用含
米(用含![]() 的代数式表示);
的代数式表示);
②![]() 的取值范围是 ;
的取值范围是 ;
(2)请你判断谁的说法正确,为什么?
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,点
中,点![]() 为
为![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,下列结论:
,下列结论:

①![]() ;
;
②![]() ;
;
③![]() ;
;
④若![]() ,则
,则![]() .
.
其中正确的结论是______________.(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
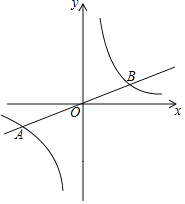
【题目】如图,在平面直角坐标系xOy中,已知正比例函数y=![]() x的图象与反比例函数y=
x的图象与反比例函数y=![]() 的图象交于A(a,-2),B两点.
的图象交于A(a,-2),B两点.
(1)求反比例函数的表达式和点B的坐标;
(2)P是第一象限内反比例函数图象上一点,过点P作y轴的平行线,交直线AB于点C,连接PO,若△POC的面积为3,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知PA=2,PB=4![]() ,以AB为边作等边△ABC,使P、C落在直线AB的两侧,连接PC.
,以AB为边作等边△ABC,使P、C落在直线AB的两侧,连接PC.
(1)如图,当∠APB=30°时,
①按要求补全图形;②求AB和PC的长.
(2)当∠APB变化时,其它条件不变,则PC的最大值为 ,此时∠APB= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区各街道居民积极响应“创文明社区”活动,据了解,某街道居民人口共有7.5万人,街道划分为A,B两个社区,B社区居民人口数量不超过A社区居民人口数量的2倍.
(1)求A社区居民人口至少有多少万人?
(2)街道工作人员调查A,B两个社区居民对“社会主义核心价值观”知晓情况发现:A社区有1.2万人知晓,B社区有1万人知晓,为了提高知晓率,街道工作人员用了两个月的时间加强宣传,A社区的知晓人数平均月增长率为m%,B社区的知晓人数第一个月增长了m%,第二个月增长了2m%,两个月后,街道居民的知晓率达到76%,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
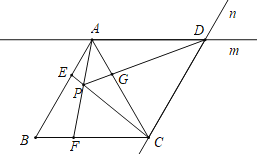
【题目】如图,在等边△ABC中,点E,F分别是边AB,BC上的动点(不与端点重合),且始终保持AE=BF,连接AF,CE相交于点P过点A作直线m∥BC,过点C作直线n∥AB,直线m,n相交于点D,连接PD交AC于点G,在点E,F的运动过程中,若![]() =
=![]() ,则
,则![]() 的值为_____.
的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )

A. (54![]() +10) cm B. (54
+10) cm B. (54![]() +10) cm C. 64 cm D. 54cm
+10) cm C. 64 cm D. 54cm
查看答案和解析>>
科目:初中数学 来源: 题型:
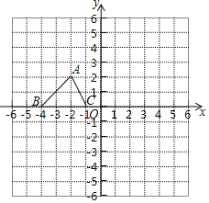
【题目】如图,已知△ABC的三个顶点的坐标分别为A(﹣2,2)、B(﹣4,0)、C(﹣1,0).
(1)请直接写出点A关于y轴对称的点D的坐标;
(2)将△ABC绕坐标原点O顺时针旋转90°得到△A1B1C1,请画出△A1B1C1并求点A在这一旋转中经过的路程.
(3)将△ABC以点C为位似中心,放大2倍得到△A2B2C,请写出一个点A2的坐标并画出△A2B2C.(所画图形必须在所给的网格内)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣2mx+m2﹣3(m是常数).
(1)证明:无论m取什么实数,该抛物线与x轴都有两个交点;
(2)设抛物线的顶点为A,与x轴两个交点分别为B,D,B在D的右侧,与y轴的交点为C.
①求证:当m取不同值时,△ABD都是等边三角形;
②当|m|≤![]() ,m≠0时,△ABC的面积是否有最大值,如果有,请求出最大值,如果没有,请说明理由.
,m≠0时,△ABC的面积是否有最大值,如果有,请求出最大值,如果没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com