
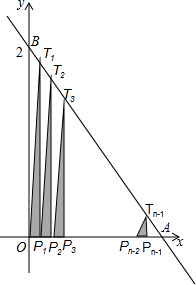
 如图,直线y=-2x+2与两坐标轴分别交于A、B两点,将线段OA分成n等份,分点分别为P1,P2,P3,…,Pn-1,过每个分点作x轴的垂线分别交直线AB于点T1,T2,T3,…,Tn-1,用S1,S2,S3,…,Sn-1分别表示Rt△T1OP1,Rt△T2P1P2,…,Rt△Tn-1Pn-2Pn-1的面积,则当n=2015时,S1+S2+S3+…+Sn-1=$\frac{1007}{2015}$.
如图,直线y=-2x+2与两坐标轴分别交于A、B两点,将线段OA分成n等份,分点分别为P1,P2,P3,…,Pn-1,过每个分点作x轴的垂线分别交直线AB于点T1,T2,T3,…,Tn-1,用S1,S2,S3,…,Sn-1分别表示Rt△T1OP1,Rt△T2P1P2,…,Rt△Tn-1Pn-2Pn-1的面积,则当n=2015时,S1+S2+S3+…+Sn-1=$\frac{1007}{2015}$. 分析 根据图象上点的坐标性质得出点T1,T2,T3,…,Tn-1各点纵坐标,进而利用三角形的面积得出S1、S2、S3、…、Sn-1,进而得出答案.
解答 解:∵P1,P2,P3,…,Pn-1是x轴上的点,且OP1=P1P2=P2P3=…=Pn-2Pn-1=$\frac{1}{n}$,
分别过点p1、p2、p3、…、pn-2、pn-1作x轴的垂线交直线y=-2x+2于点T1,T2,T3,…,Tn-1,
∴T1的横坐标为:$\frac{1}{n}$,纵坐标为:2-$\frac{2}{n}$,
∴S1=$\frac{1}{2}$×$\frac{1}{n}$(2-$\frac{2}{n}$)=$\frac{1}{n}$(1-$\frac{1}{n}$)
同理可得:T2的横坐标为:$\frac{2}{n}$,纵坐标为:2-$\frac{4}{n}$,
∴S2=$\frac{1}{n}$(1-$\frac{2}{n}$),
T3的横坐标为:$\frac{3}{n}$,纵坐标为:2-$\frac{6}{n}$,
S3=$\frac{1}{n}$(1-$\frac{3}{n}$)
…
Sn-1=$\frac{1}{n}$(1-$\frac{n-1}{n}$)
∴S1+S2+S3+…+Sn-1=$\frac{1}{n}$[n-1-$\frac{1}{2}$(n-1)]=$\frac{1}{2}$×$\frac{1}{n}$(n-1)=$\frac{n-1}{2n}$,
∵n=2015,
∴S1+S2+S3+…+S2014=$\frac{1}{2}$×$\frac{1}{2015}$×2014=$\frac{1007}{2015}$.
故答案为:$\frac{1007}{2015}$.
点评 此题考查了一次函数函数图象上点的坐标特点,先根据题意得出T点纵坐标变化规律进而得出S的变化规律,得出图形面积变化规律是解题关键.


科目:初中数学 来源: 题型:解答题
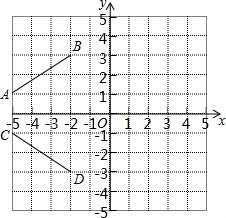 如图,在平面直角坐标系中,线段AB的两个端点是A(-5,1),B(-2,3),线段CD的两个端点是C(-5,-1),D(-2,-3).
如图,在平面直角坐标系中,线段AB的两个端点是A(-5,1),B(-2,3),线段CD的两个端点是C(-5,-1),D(-2,-3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 台风是一种自然灾害,它以台风中心为圆心在数十千米范围内形成气旋风暴,有极强的破坏力,据气象观察,距沿海某城市A正南256千米的B处有一台风中心,其中心最大风力为12级,每远离台风中心20千米,风力就会减弱一级,该台风中心正以15千米/时的速度沿北偏东30°方向向C移动,且台风中心风力不变,若城市受到的风力达到或超过四级,则称受台风影响.
台风是一种自然灾害,它以台风中心为圆心在数十千米范围内形成气旋风暴,有极强的破坏力,据气象观察,距沿海某城市A正南256千米的B处有一台风中心,其中心最大风力为12级,每远离台风中心20千米,风力就会减弱一级,该台风中心正以15千米/时的速度沿北偏东30°方向向C移动,且台风中心风力不变,若城市受到的风力达到或超过四级,则称受台风影响.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=$\frac{1}{2x}$ | B. | y=$\frac{2}{x}$ | C. | y=$\frac{1}{8x}$ | D. | y=$\frac{8}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
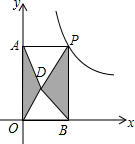 如图,点P是反比例函数y=$\frac{6}{x}$(x>0)的图象上的任意一点,过点P分别作两坐标轴的垂线,与坐标轴构成矩形OAPB,点D是矩形OAPB内任意一点,连接DA、DB、DP、DO,则图中阴影部分的面积是( )
如图,点P是反比例函数y=$\frac{6}{x}$(x>0)的图象上的任意一点,过点P分别作两坐标轴的垂线,与坐标轴构成矩形OAPB,点D是矩形OAPB内任意一点,连接DA、DB、DP、DO,则图中阴影部分的面积是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com