
【题目】解下列不等式或不等式组:
(1)5x17x3;
(2)![]()
![]() ;
;
(3) ;
;
(4)
【答案】(1)x≥2;(2)x≤8;(3)x<-5;(4)![]() <x<2
<x<2
【解析】
(1)直接根据不等式的性质解答即可;
(2)直接根据不等式的性质解答即可;
(3)应先解每个不等式,再求其公共部分;
(4)应先解每个不等式,再求其公共部分
(1)5x17x3
移项得,5x-7x≤-3-1,
合并同类项得,-2x≤-4,
系数化为1得,x≥2.
(2)![]()
![]()
去分母得,6(x-1)-4(x+1)≥3(x-2)-12,
去括号得,6x-6-4x-4≥3x-6-12,
移项得,6x-4x-3x≥-6-12+6+4,
合并同类项得,-x≥-8,
系数化为1得,x≤8.
(3)
由①得,6-3(x+1)>12-2(x+2),
6-3x-3>12-2x-4,
x<-5,
由②得,x-5≥6x-2,
x-6x≥5-2,
-5x≥3,
x≤-![]() .
.
所以,不等式的解集为x<-5.
(4)
由①得,2x-1<4-8+4x,
2x-4x<4-8+1,
-2x<-3,
x>![]() ,
,
由②得,x-4>2x-6,
x-2x>4-6,
-x>-2,
x<2.
所以,不等式的解集为![]() <x<2.
<x<2.


科目:初中数学 来源: 题型:
【题目】贺岁片《流浪地球》被称为开启了中国科幻片的大门,2019也被称为中国科幻片的元年.某电影院为了全面了解观众对《流浪地球》的满意度情况,进行随机抽样调查,分为四个类别:A.非常满意;B.满意;C.基本满意;D.不满意.依据调查数据绘制成图1和图2的统计图(不完整).根据以上信息,解答下列问题:
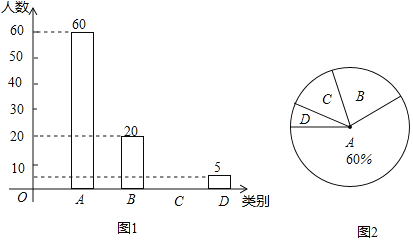
(1)本次接受调查的观众共有 人;
(2)扇形统计图中,扇形C的圆心角度数是 .
(3)请补全条形统计图;
(4)春节期间,该电影院来观看《流浪地球》的观众约3000人,请估计观众中对该电影满意(A、B、C类视为满意)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
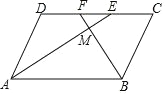
【题目】如图,在 ABCD 中,AE、BF 分别平分∠DAB 和∠ABC,交 CD 于点 E、F,AE、BF 相交于点 M.
(1)求证:AE⊥BF;
(2)判断线段 DF 与 CE 的大小关系,并予以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2-2amx+am2+2m+4的顶点P在一条定直线l上.
(1)直接写出直线l的解析式;
(2)若存在唯一的实数m,使抛物线经过原点.
①求此时的a和m的值;
②抛物线的对称轴与x轴交于点A,B为抛物线上一动点,以OA、OB为边作□OACB,若点C在抛物线上,求B的坐标.
(3)抛物线与直线l的另一个交点Q,若a=1,直接写出△OPQ的面积的值或取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级某班部分学生植树,若每人平均植树8棵,还剩7棵;若每人植树9棵,则有一名学生植树的棵树多于3棵而小于6棵.若设学生人数为x人,则植树棵树为(8x7)人,则下面给出的不等式(组)中,能准确求出学生人数与种植树木数量的是( )
A.8x769(x1)B.8x739(x1)
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)停车难已成为合肥城市病之一,主要表现在居住停车位不足,停车资源结构性失衡,中心城区供需差距大等等.如图是张老师的车与墙平行停放的平面示意图,汽车靠墙一侧OB与墙MN平行且距离为0.8米,已知小汽车车门宽AO为 1.2 米,当车门打开角度∠AOB为40°时,车门是否会碰到墙?请说明理由.(参考数据:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,AB=8,AD⊥BC,点E为线段AD上的动点,连接CE,以CE为边作等边△CEF,连接DF,则线段DF的最小值为( )

A.![]() B.4C.2D.无法确定
B.4C.2D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:
①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>﹣1时,y的值随x值的增大而增大.
其中正确的结论有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,点
,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的点,点
上的点,点![]() 是一动点.记
是一动点.记![]() 为
为![]() ,
,![]() 为
为![]() ,
,![]() 为
为![]() .
.

(1)若点![]() 在线段
在线段![]() 上,且
上,且![]() ,如图1,则
,如图1,则![]() _____________;
_____________;
(2)若点![]() 在边
在边![]() 上运动,如图2所示,请猜想
上运动,如图2所示,请猜想![]() ,
,![]() ,
,![]() 之间的关系,并说明理由;
之间的关系,并说明理由;
(3)若点![]() 运动到边
运动到边![]() 的延长线上,如图3所示,则
的延长线上,如图3所示,则![]() ,
,![]() ,
,![]() 之间又有何关系?请直接写出结论,不用说明理由.
之间又有何关系?请直接写出结论,不用说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com