
����Ŀ����1����ͼ1,��������ABCD��,��E,F�ֱ��ڱ�BC,CD��,AE,BF���ڵ�O,��AOF��90��.
��֤��BF��AE.

(2) ��ͼ2,������ABCD�߳�Ϊ12������������MN�۵���ʹ��A����DC���ϵĵ�E������DE=5�����ۺ�MN�ij���

(3) ��֪��E,H,F,G�ֱ��ھ���ABCD�ı�AB,BC,CD,DA�ϣ�EF,GH���ڵ�O,
��FOH��90��,EF��4. ֱ��д����������Ĵ𰸣�
����ͼ3,����ABCD��2��ȫ�ȵ����������,�� GH=___________��
����ͼ4,����ABCD��n��ȫ�ȵ����������,�� GH=___________��(��n�Ĵ���ʽ��ʾ).

���𰸡���1��֤����������2��13��3��8�� 4n
�������������������1�����������ε����ʿɵ�AB=BC����ABC=��BCD=90�����ٸ���ͬ�ǵ������������EAB=��FBC��Ȼ���������DZ߽���֤����ABE����BCFȫ�ȣ��ٸ���ȫ�������ζ�Ӧ�����֤�����ɣ�
��2������AE������N��NH��AD��H�����ݷ��۵����ʿɵ�AE��NM��Ȼ�������DAE=��MNH�����������DZ߽���֤����ADE����NHMȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�AE=MN��Ȼ�����ù��ɶ�����ʽ���AE���Ӷ��ý⣻
��3������F��FM��AB��M������G��GN��BC��N���������������ζ�Ӧ�߳ɱ�����⼴�ɣ�
�����������1��֤������ͼ�����ı���ABCDΪ�����Σ�
��AB=BC����ABC=��BCD=90��
��� EAB+��AEB=90����
�ߡ�EOB=��AOF=90�������FBC+��AEB=90����
���EAB=��FBC
���ABE�ա�BCF����AE = BF
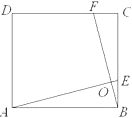
(2)����AE,����N��NH��AD,֤����MNH��EAD
��MN=AE
�ɹ��ɶ�����AE=13, ��MN=13
��3��8�� 4n


 ��ĩ�����ϵ�д�
��ĩ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������y=��2x2����ƽ��1����λ���ȣ�������ƽ��1����λ�������õ������߽���ʽΪ�� ��
A.y=��2��x+1��2
B.y=��2��x+1��2+2
C.y=��2��x��1��2+2
D.y=��2��x��1��2+1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���û�������ͼ�ķ�ʽ��ͼ�Σ�

��1��ͼ�� ��������ͼ���� ��������ͼ���� ������.
��2��������ķ���������ȥ����100��ͼ�����ж��ٸ�������
��3����n��n��1����������ͼ�����ж��ٸ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
(1)��(-4)-(+11)-(-9) (2). 12-(-18)��(-12)-15
(3). ![]() (4).
(4). ![]()
(5)��|-![]() |-(-2.5)+1-|1-
|-(-2.5)+1-|1-![]() | (6)��
| (6)��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������1����20+����18����12 +10�� ��2��![]()
��3��![]() �� ��4����2.5��17��(��4) ��(��0.1)
�� ��4����2.5��17��(��4) ��(��0.1)
��5��(��36) ��4��5��(��1.2) �� ��6��![]()
��7�� ��8��
��8��![]()
(9) ![]()
![]() ����.+
����.+ ![]() ��10��
��10��![]()
![]() ����.+
����.+ ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����3m��ʾ����3m,��ô-2m��6m�ֱ��ʾ( )
A. ����2m,������6m B. ����2m,����6m
C. ������2m,������6m D. ������2m,����6m
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com