如图，△ABC的三边AB，BC，CA的长分别是20，30，40，其三条角平分线将△ABC分为三个三角形，则S△ABO∶S△BCO∶S△CAO等于_______
千里马走向假期期末仿真试卷寒假系列答案科目：初中数学 来源：山东省德州市2016-2017学年七年级下学期第二次月考数学试卷 题型：单选题
如图，AB∥CD，∠BAC与∠DCA的平分线相交于点G，GE⊥AC于点E，F为AC上的一点，且FA＝FG＝FC，GH⊥CD于H.下列说法：①AG⊥CG；②∠BAG＝∠CGE；③S△AFG＝S△CFG；④若∠EGH︰∠ECH＝2︰7，则∠EGF＝50°.其中正确的有（ ）
A. ①②③④ B. ②③④ C. ①③④ D. ①②④
查看答案和解析>>
科目：初中数学 来源：江西省吉安市2017届九年级中考最后一模数学试卷 题型：解答题
太阳能光伏建筑是现代绿色环保建筑之一，老张准备把自家屋顶改建成光伏瓦面，改建前屋顶截面△ABC如图2所示，BC=10米，∠ABC=∠ACB=36°，改建后顶点D在BA的延长线上，且∠BDC=90°，求改建后南屋面边沿增加部分AD的长．（结果精确到0.1米）
（参考数据：sin18°≈0.31，cos18°≈0.95．tan18°≈0.32，sin36°≈0.59．cos36°≈0.81，tan36°≈0.73）
查看答案和解析>>
科目：初中数学 来源：北京昌平临川育人学校2016-2017学年七年级6月月考数学试卷 题型：解答题
数学课上，张老师出示了问题：如图1，四边形ABCD是正方形， 
， 
， 
∥
， 
∥
点E是边BC的中点． 
，且EF交正方形外角
的角平分线CF于点F，求证：AE=EF．
经过思考，小明展示了一种正确的解题思路：取AB的中点M，连接ME，则AM=EC，易证
，所以
．
在此基础上，同学们作了进一步的研究：
（1）
小颖提出：如图2，如果把“点E是边BC的中点”改为“点E是边BC上（除B，C外）的任意一点”，其它条件不变，那么结论“AE=EF”仍然成立，你认为小颖的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由；
（2）小华提出：如图3，点E是BC的延长线上（除C点外）的任意一点，其他条件不变，结论“AE=EF”仍然成立．你认为小华的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由．
查看答案和解析>>
科目：初中数学 来源：北京昌平临川育人学校2016-2017学年七年级6月月考数学试卷 题型：解答题
如图AB、CD相交于点O，AO＝BO，AC∥DB。那么OC与OD相等吗？说明你的理由。
小明的解题过程如下，请你说明每一步的理由。
【解析】
OC＝OD，理由如下：
∵AC∥DB （ 已 知 ）
∴∠A=∠B ∠C=∠D （ ）
在△AOC和△BOD中
∴△AOC≌△BOD （ ）
∴OC＝OD （ ）
查看答案和解析>>
科目：初中数学 来源：北京昌平临川育人学校2016-2017学年七年级6月月考数学试卷 题型：单选题
如图，AE⊥BC于E，BF⊥AC于F，CD⊥AB于D，则△ABC中AC边上的高是垂线段（ ）
A. AE B. CD C. BF D. AF
查看答案和解析>>
科目：初中数学 来源：江苏省2016-2017学年八年级5月月考数学试卷 题型：解答题
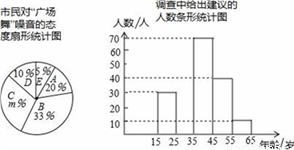
近年来，各地“广场舞”噪音干扰的问题倍受关注，相关人员对本地区15﹣65岁年龄段的市民进行了随机调查，并制作了如图相应的统计图．市民对“广场舞”噪音干扰的态度有以下五种：A．没影响 B．影响不大 C．有影响，建议做无声运动 D．影响很大，建议取缔 E．不关心这个问题
根据以上信息解答下列问题：
（1）根据统计图填空求m的值为多少，A区域所对应的扇形圆心角为多少度；
（2）在此次调查中，“不关心这个问题”的有25人，请问一共调查了多少人？
（3）此次调查中，C、D两种给出了建议，请将调查中给出建议的人数条形统计图补充完整．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
____________________．