
【题目】如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,P1,P2,P3,P4,P5是△DEF边上的5个格点,请按要求完成下列各题:
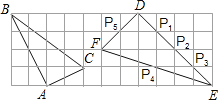
(1)试证明三角形△ABC为直角三角形;
(2)判断△ABC和△DEF是否相似,并说明理由;
(3)画一个三角形,使它的三个顶点为P1,P2,P3,P4,P5中的3个格点并且与△ABC相似(要求:不写作法与证明).
【答案】(1)证明见解析;(2)相似,(3)作图见解析.
【解析】
试题(1)利用网格得出AB2=20,AC2=5,BC2=25,再利用勾股定理逆定理得出答案即可;
(2)利用AB=2![]() ,AC=
,AC=![]() ,BC=5以及DE=4
,BC=5以及DE=4![]() ,DF=2
,DF=2![]() ,EF=2
,EF=2![]() ,利用三角形三边比值关系得出即可;
,利用三角形三边比值关系得出即可;
(3)根据△P2P4P5三边与△ABC三边长度得出答案即可.
解:(1)∵AB2=20,AC2=5,BC2=25;
∴AB2+AC2=BC2,
根据勾股定理的逆定理得△ABC 为直角三角形;
(2)△ABC和△DEF相似.
由(1)中数据得AB=2![]() ,AC=
,AC=![]() ,BC=5,
,BC=5,
DE=4![]() ,DF=2
,DF=2![]() ,EF=2
,EF=2![]() .
.
![]() =
=![]() =
=![]() =
=![]() =
=![]() ,
,
∴△ABC∽△DEF.
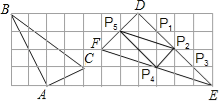
(3)如图:连接P2P5,P2P4,P4P5,
∵P2P5=![]() ,P2P4=
,P2P4=![]() ,P4P5=2
,P4P5=2![]() ,
,
AB=2![]() ,AC=
,AC=![]() ,BC=5,
,BC=5,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
∴△ABC∽△P2P4P5.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
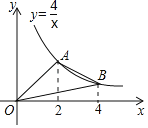
【题目】如图,A,B是反比例函数y=![]() 在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是( )
在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
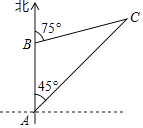
【题目】一艘货轮以34海里/时的速度在海面上向正南方向航行,当它行驶至B处时,某观察者发现在货轮的北偏东75°方向有一灯塔C;货轮继续向南航行1.5小时后到达A处,某观察者再次发现灯塔C在货轮的东北方向.求此时货轮与灯塔C的距离.(结果保留到个位)(参考数据:sin75°≈0.97,cos75°≈0.29,tan75°≈3.73,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为5,点A的坐标为(﹣4,0),点B在y轴上,若反比例函数y=![]() (k≠0)的图象过点C,则该反比例函数的表达式为_______.
(k≠0)的图象过点C,则该反比例函数的表达式为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于![]() 的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )
的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )

A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
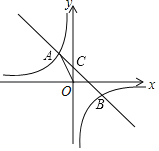
【题目】如图,在平面直角坐标系中,一次函数y=ax+b的图象与反比例函数y=![]() (k为常数,k≠0)的图象交于二、四象限内的A、B两点,与y轴交于C点.点A的坐标为(m,3),点B与点A关于y=x成轴对称,tan∠AOC=
(k为常数,k≠0)的图象交于二、四象限内的A、B两点,与y轴交于C点.点A的坐标为(m,3),点B与点A关于y=x成轴对称,tan∠AOC=![]() .
.
(1)求k的值;
(2)直接写出点B的坐标,并求直线AB的解析式;
(3)P是y轴上一点,且S△PBC=2S△AOB,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
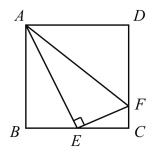
【题目】如图,在正方形 ABCD 中,E是BC的中点,F是CD上一点,AE⊥EF.有下列结论:
①∠BAE=30°;
②射线FE是∠AFC的角平分线;
③CF=![]() CD;
CD;
④AF=AB+CF.
其中正确结论的个数为( )
A.1 个B.2 个C.3 个D.4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
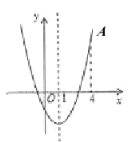
【题目】二次函数![]() (
(![]() )的大致图象如图所示,顶点坐标为
)的大致图象如图所示,顶点坐标为![]() ,点
,点![]() 是该抛物线上一点,若点
是该抛物线上一点,若点![]() 是抛物线上任意一点,有下列结论:
是抛物线上任意一点,有下列结论:
①![]() ;
;
②若![]() ,则
,则![]() ;
;
③若![]() ,则
,则![]() ;
;
④若方程![]() 有两个实数根
有两个实数根![]() 和
和![]() ,且
,且![]() ,则
,则![]() .
.
其中正确结论的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,王老师让同学们对给定的正方形ABCD,如图.建立合适的平面直角坐标系,并表示出各顶点的坐标.下面是4名同学表示各顶点坐标的结果:
甲同学:A(0,1),B(0,0),C(1,0),D(1,1);
乙同学:A(0,0),B(0,-1),C(1,-1),D(1,0);
丙同学:A(1,0),B(1,-2),C(3,-2),D(3,0);
丁同学:A(-1,2),B(-1,0),C(0,0),D(0,2);
上述四名同学表示的结果中,四个点的坐标都表示正确的同学是( )

A. 甲、乙、丙B. 乙、丙、丁C. 甲、丙D. 甲、乙、丙、丁
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com