已知等边△ABC的边长为6,A点坐标为(2,0),B点在x轴上,C点在第一象限.
(1)求顶点B、C的坐标;
(2)以点B为中心,将等边△ABC顺时针旋转60°,则旋转后的等边三角形与原来的等边三角形组成一个四边形,求这个四边形的第四个顶点坐标;
(3)求(2)中所得到的四边形的对角线的长.
分析:(1)根据A点坐标及AB的长,易求得点B的坐标,进而可结合等边三角形的性质求得C点坐标.
(2)由于△ABC是等边三角形,若旋转角度为60°,那么CD∥AB,因此只需将点C向右平移AB个单位即可求得点D的坐标.
(3)显然四边形ABDC是菱形,那么它的对角线互相垂直平分,即可通过解直角三角形求得两条对角线的长.
解答:
解:(1)如图;
∵A点坐标为(2,0),|AB|=6,
∴|OB|=8,∴B点坐标为(8,0).(2分)
作CH⊥AB于H,∵|AH|=3,|AC|=6,
∴
|CH|====3.
∴C点坐标为
(5,3).(4分)
(2)以B为中心,将等边△ABC顺时针旋转60°,则A点旋转到C点,C点旋转到D点,如右图,则D点坐标为
(11,3).
(3)如右图,∵|AB|=|BD|=|DC|=|CA|=6,
∴四边形ABDC是菱形.
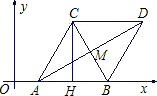
∵△ABC是等边三角形,∴对角线|BC|=6.(6分)
连接AD,则AD⊥BC,若AD与BC交于M,则
AM=×6=3.
∴
|AD|=6,即对角线BC=6,AD=6
.(8分)
(注:本题不画图不扣分)
点评:此题主要考查了等边三角形的性质、旋转的性质、菱形的判定和性质以及解直角三角形等知识,难度适中.

 解:(1)如图;
解:(1)如图;


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案 11、如图,已知等边△ABC的边长为8,P是△ABC内一点,PD∥AC,PE∥AD,PF∥BC,点D,E,F分别在AB,BC,AC上,则PD+PE+PF=
11、如图,已知等边△ABC的边长为8,P是△ABC内一点,PD∥AC,PE∥AD,PF∥BC,点D,E,F分别在AB,BC,AC上,则PD+PE+PF=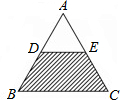 (2011•辽阳)如图,已知等边△ABC的面积为1,D、E分别为AB、AC的中点,若向图中随机抛掷一枚飞镖,飞镖落在阴影区域的概率是(不考虑落在线上的情形)( )
(2011•辽阳)如图,已知等边△ABC的面积为1,D、E分别为AB、AC的中点,若向图中随机抛掷一枚飞镖,飞镖落在阴影区域的概率是(不考虑落在线上的情形)( ) 动,第一次回到点A处停止运动,设AP=S,用t表示运动时间.
动,第一次回到点A处停止运动,设AP=S,用t表示运动时间.