练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

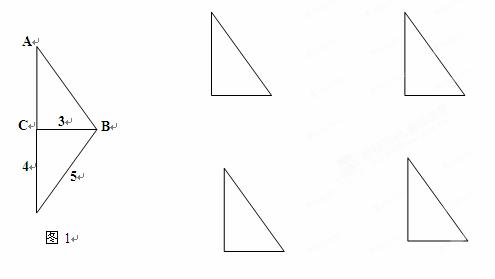
    探究：如图，在△中，，，，在△的外部拼接一个合适的三角形，使得拼成的图形是一个等腰三角形，如图（1）所示。要求再给出的的四个备用图中分别画出四种与示例不同的拼接方法，并在图中标明拼接的直角三角形的三边长。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，在△ABC中，∠C=90°，BC=8，AC=6，另有一直角梯形DEFH（HF∥DE，∠HDE=90°）的底边DE落在CB上，腰DH落在CA上，且DE=4，∠DEF=∠CBA，AH：AC=2：3
    （1）延长HF交AB于G，求△AHG的面积．
    （2）操作：固定△ABC，将直角梯形DEFH以每秒1个单位的速度沿CB方向向右移动，直到点D与点B重合时停止，设运动的时间为t秒，运动后的直角梯形为DEFH′（如图）．
    探究1：在运动中，四边形CDH′H能否为正方形？若能，请求出此时t的值；若不能，请说明理由．
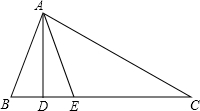    探究2：在运动过程中，△ABC与直角梯形DEFH′重叠部分的面积为y，求y与t的函数关系．精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    精英家教网如图，在△ABC中，AD⊥BC，AE平分∠BAC，∠B=70°，∠C=30°．
    （1）求∠BAE的度数；
    （2）求∠DAE的度数；
    （3）探究：小明认为如果只知道∠B-∠C=40°，也能得出∠DAE的度数？你认为可以吗？若能，请你写出求解过程；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•长春一模）感知：如图①，在菱形ABCD中，AB=BD，点E、F分别在边AB、AD上．若AE=DF，易知△ADE≌△DBF．
    探究：如图②，在菱形ABCD中，AB=BD，点E、F分别在BA、AD的延长线上．若AE=DF，△ADE与△DBF是否全等？如果全等，请证明；如果不全等，请说明理由．
    拓展：如图③，在?ABCD中，AD=BD，点O是AD边的垂直平分线与BD的交点，点E、F分别在OA、AD的延长线上．若AE=DF，∠ADB=50°，∠AFB=32°，求∠ADE的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

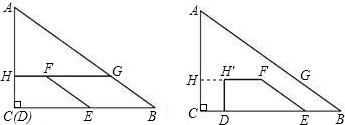
    （2013•广阳区一模）九年级数学兴趣小组近期开展了对运动型问题的探究．小明同学提供了一个这样的背景：如图，在?ABCD中，AB=AC=10cm，sin∠ACB=
    45
    ，动点O从A出发以1cm/s的速度沿AC方向向点C匀速运动，同时线段EF从与线段CB重合的位置出发以1cm/s的速度沿BA方向向点C匀速运动．在运动过程中，EF交AC于点G，连接OE、OF．设运动时间为ts（0＜t＜10），请你解决以下问题：
    （1）当t为何值时，点O与点G重合？
    （2）当点O与点G不重合时，判断△OEF的形状，并说明理由．             
    （3）当0＜t＜5时，
        ①在上述运动过程中，五边形BCEOF的面积是否为定值？如果是，求出五边形BCEOF的面积；如果不是，请说明理由．
        ②△EOG的面积是否存在最大值？若存在，请求出最大值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    解决下面问题：
    如图，在△ABC中，∠A是锐角，点D，E分别在AB，AC上，且∠DCB=∠EBC=
    12
    ∠A，BE与CD相交于点O，探究BD与CE之间的数量关系，并证明你的结论．

    小新同学是这样思考的：
    在平时的学习中，有这样的经验：假如△ABC是等腰三角形，那么在给定一组对应条件，如图a，BE，CD分别是两底角的平分线（或者如图b，BE，CD分别是两条腰的高线，或者如图c，BE，CD分别是两条腰的中线）时，依据图形的轴对称性，利用全等三角形和等腰三角形的有关知识就可证得更多相等的线段或相等的角．这个问题也许可以通过添加辅助线构造轴对称图形来解决．请参考小新同学的思路，解决上面这个问题．

    查看答案和解析>>

    同步练习册答案