练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

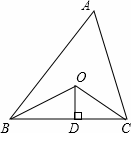
    如图所示，已知△ABC的周长是21，OB，OC分别平分∠ABC和∠ACB，OD⊥BC于D，且OD=3，则△ABC的面积是       ．


    31.5   解析：作OE⊥AC，OF⊥AB，垂足分别为E、F，连接OA，

    ∵ OB，OC分别平分∠ABC和∠ACB，OD⊥BC，

    ∴ OD=OE=OF.

    ∴

    =×OD×BC+×OE×AC+×OF×AB

    =×OD×（BC+AC+AB）

    =×3×21=31.5．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    一只口袋中放着若干只红球和白球，这两种球除了颜色以外没有任何其他区别，袋中的球已经搅匀，蒙上眼睛从口袋中取出一只球，取到红球的概率是．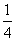

    （1）取到白球的概率是多少？

    （2）如果袋中的白球有18只，那么袋中的红球有多少只？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知点与点关于轴对称，则        ，        ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    小华在电话中问小明：“已知一个三角形三边长分别是4，9，12，如何求这个三角形的面积？小明提示说：“可通过作最长边上的高来求解.”小华根据小明的提示作出的图形正确的是（    ）

        A.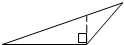    B.

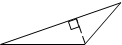        C.     D.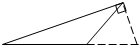

    查看答案和解析>>

    科目：初中数学 来源： 题型：


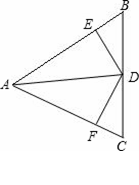
    如图所示，在△ABC中，AB=AC，AD是△ABC的角平分线，DE⊥AB，DF⊥AC，垂足分别是E，F．则下面结论中①DA平分∠EDF；②AE=AF，DE=DF；③AD上的点到B、C两点的距离相等；④图中共有3对全等三角形，正确的有：      .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    认真阅读下面关于三角形内外角平分线所夹的探究片段，完成所提出的问题．

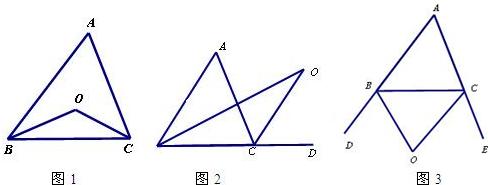
    探究1：如图1，在△ABC中，O是∠ABC与∠ACB的平分线BO和CO的交点，通过分析发现∠BOC=90°+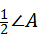，理由如下：

    ∵BO和CO分别是∠ABC和∠ACB的角平分线

    ∴

    ∴

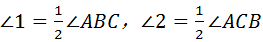
    又∵∠ABC+∠ACB=180°﹣∠A

    ∴

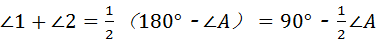
    ∴∠BOC=180°﹣（∠1+∠2）=180°﹣（90°﹣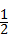∠A）

    =.

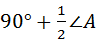    探究2：如图2中，O是∠ABC与外角∠ACD的平分线BO和CO的交点，试分析∠BOC与∠A有怎样的关系？请说明理由．

    探究3：如图3中，O是外角∠DBC与外角∠ECB的平分线BO和CO的交点，则∠BOC与∠A有怎样的关系？（只写结论，不需证明）

    结论：　     　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，△是由△经过平移后得到的，则平移的距离是（     ）

    A.线段的长度            B.线段的长度     

    C.线段的长度            D.线段的长度          

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，要测量两堵墙所形成的∠的度数，但人不能进入围墙，如何测量请你写出两种不同的测量方法，并说明其几何道理．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一块长方形菜地的面积是150m2，如果它的长减少5m，那么菜地就变成正方形，若设原菜地的长为x m，则可列方程为：         ．

    查看答案和解析>>

    同步练习册答案