
 如图,一块长为20米,宽为8米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56米2,两块绿地之间及周边留有宽度相等的人形通道.
如图,一块长为20米,宽为8米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56米2,两块绿地之间及周边留有宽度相等的人形通道.分析 (1)设人行通道的宽度为x米.将两个绿地平移到一起,然后用含x的是表示绿地的长与宽,最后依据面积为56平方米列方程求解即可;
(2)设园丁原计划每小时完成x米2.接下来,依据园丁按计划完成40平方米与时间完成40平方米的时间差为1小时列方程求解即可.
解答 解:(1)设人行通道的宽度为x米.
根据题意得:(20-3x)(8-2x)=56.
整理得:3x2-32x+52=0.
解得:x1=2,x2=$\frac{26}{3}$(舍去).
答:人行通道的宽2米.
(2)设园丁原计划每小时完成x米2.
$\frac{40}{x}=\frac{40}{1.25x}$+1.
解得:x=8.
经检验x=8是原方程的解.
答:园丁原计划每小时完成8米2.
根据题意得:8米2
点评 本题主要考查的是一元二次方程和分式方程的应用,根据题意列出关于x的方程是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$•$\sqrt{3}$=$\sqrt{6}$ | B. | $\sqrt{8}$÷$\sqrt{2}$=2 | C. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | D. | (-$\sqrt{3}$)2=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3cm,5cm,8cm | B. | 1cm,2cm,3cm | C. | 4cm,5cm,10cm | D. | 3cm,4cm,5cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
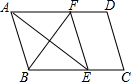 如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为( )
如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为( )| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com