
【题目】完成下面的证明.

如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知)
且∠1=∠CGD(_______)
∴∠2=∠CGD(等量代换)
∴CE∥BF(_______)
∴∠_____=∠BFD(_______)
又∵∠B=∠C(已知)
∴∠BFD=∠B(_______)
∴AB∥CD(_______)
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
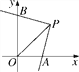
【题目】如图,在平面直角坐标系xOy中,三角板的直角顶点P的坐标为(2,2),一条直角边与x轴的正半轴交于点A,另一直角边与y轴交于点B,三角板绕点P在坐标平面内转动的过程中,当△POA为等腰三角形时,请写出所有满足条件的点B的坐标__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)是否存在点M,使△OMC的面积是△OAC的面积的![]() ?若存在求出此时点M的坐标;若不存在,说明理由.
?若存在求出此时点M的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两条直线相交所成的四个角分别满足下列条件之一,其中不能判定这两条直线垂直的条件是( )
A.两对对顶角分别相等B.有一对对顶角互补
C.有一对邻补角相等D.有三个角相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,∠AOB=90°,点C在射线OA上,CD∥OE.
(1)如图1,若∠OCD=120°,求∠BOE的度数;
(2)把“∠AOB=90°”改为“∠AOB=120°”,射线OE沿射线OB平移,得O′E,其他条件不变,(如图2所示),探究∠OCD、∠BO′E的数量关系;
(3)在(2)的条件下,作PO′⊥OB垂足为O′,与∠OCD的平分线CP交于点P,若∠BO′E=α,请用含α的式子表示∠CPO′(请直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形ABC与三角形A'B'C'在平面直角坐标系中的位置如图:
(1)分别写出下列各点的坐标:A'_____; B'_____;C'_____;
(2)三角形A'B'C'由三角形ABC经过怎样的平移得到?___________;
(3)若点P(a,b)是三角形ABC内部一点,则平移后三角形A'B'C'内的对应点P'的坐标为_________;
(4)求三角形ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一堆有红、白两种颜色的球若干个,已知白球的个数比红球少,但白球的2倍比红球多.若把每一个白球都记作“2”,每一个红球都记作“3”,则总数为“60”,那么这两种球各有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据不等式的基本性质,把下列不等式化成“x>a”或“x<a”的形式:
(1)4x>3x+5 (2)-2x<17
(3)0.3x<-0.9 (4)x<![]() x-4
x-4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com