
| 方程 | 方程的根x1、x2 |
| x2-5x+6=0 | x1=2,x2=3 |
| 6x2-5x+1=0 | x1=$\frac{1}{2}$,x2=$\frac{1}{3}$ |
| x2-7x+10=0 | x1=2,x2=5 |
| 10x2-7x+1=0 | x1=$\frac{1}{2}$,x2=$\frac{1}{5}$ |
分析 (1)分析表中方程的根与系数的关系:交换一个一元二次方程的二次项与常数项的系数所得的方程的解是原方程的解倒数.
(2)利用公式法解一元二次方程ax2-bx+c=0与cx2-bx+a=0的两根,然后分析它们的根的数量关系即可.
(3)根据(1)与(2)的结论求出一元二次方程a2-3a+2=0和2b2-3b+1=0的两个根,再根据ab≠1,分析a、b的取值即可求出代数式$\frac{ab+a-1}{b}$的值.
解答 解:(1)根据表中方程的根的规律:交换一个一元二次方程的二次项与常数项的系数所得的方程的解是原方程的解倒数,
故答案为:x1=$\frac{1}{m}$,x2=$\frac{1}{n}$.
(2)∵一元二次方程ax2-bx+c=0(a、c均不为0)的两个实数根为m、n,
∴m=$\frac{b+\sqrt{{b}^{2}-4ac}}{2a}$,n=$\frac{b-\sqrt{{b}^{2}-4ac}}{2a}$,
又∵一元二次方程cx2-bx+a=0中,
x1=$\frac{b+\sqrt{{b}^{2}-4ac}}{2c}$,x2=$\frac{b-\sqrt{{b}^{2}-4ac}}{2c}$,
∴m•x2═$\frac{b+\sqrt{{b}^{2}-4ac}}{2a}$•$\frac{b-\sqrt{{b}^{2}-4ac}}{2c}$=$\frac{{b}^{2}-({b}^{2}-4ac)}{4ac}$=1
n•x1=$\frac{b-\sqrt{{b}^{2}-4ac}}{2a}$•$\frac{b+\sqrt{{b}^{2}-4ac}}{2c}$=1
∴x1=$\frac{1}{n}$,x2=$\frac{1}{m}$
即:如果一元二次方程ax2-bx+c=0(a、c均不为0)的两个实数根为m、n,那么cx2-bx+a=0的两根是 $\frac{1}{m}$,$\frac{1}{n}$;
(3)解一元二次方程a2-3a+2=0,得:a1=2或 a=1,
则:由(1)知一元二次方程2b2-3b+1=0的解为 b=$\frac{1}{2}$或b=1
∵ab≠1,
∴ab=2或ab=$\frac{1}{2}$,即:a=2,b=1或a=1,b=$\frac{1}{2}$
∴当a=2,b=1时,$\frac{ab+a-1}{b}$=$\frac{2+2-1}{1}$=3
当或a=1,b=$\frac{1}{2}$时,$\frac{ab+a-1}{b}$=$\frac{\frac{1}{2}+1-1}{\frac{1}{2}}=1$
∴$\frac{ab+a-1}{b}$的值为3或1.
点评 本题考查了一元二次方程的根与系数的关系,解题的关键是认真分析表中方程的根与系数的关系结合一元二次方程的解法加以论证与应用.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:选择题
| A. | -2和|-2| | B. | -2和$-\frac{1}{2}$ | C. | 2和$\frac{1}{2}$ | D. | -(-2)和|-2| |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a≥b | B. | a≤b | C. | a>b | D. | a<b |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
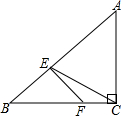 如图,在△ABC中,AC=BC,∠BCA=90°,点E是斜边AB上的一点,作EF⊥AB交边BC于点F连结EC,若BE:EA=1:2,则∠ECF的余弦值为( )
如图,在△ABC中,AC=BC,∠BCA=90°,点E是斜边AB上的一点,作EF⊥AB交边BC于点F连结EC,若BE:EA=1:2,则∠ECF的余弦值为( )| A. | $\frac{2\sqrt{5}}{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\sqrt{5}$ | D. | -$\frac{\sqrt{5}}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $±\sqrt{9}=±3$ | B. | -($\sqrt{2}$)2=4 | C. | $\root{3}{-9}=-3$ | D. | $\sqrt{{{(-2)}^2}}=-2$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com