
 如图,菱形ABCD中,∠A=60°,边长为4厘米,动点P从A出发,以1厘米/秒的速度沿A-B-C运动,在P出发1秒后,点Q以同样的速度沿相同的路线运动,过点P、Q的直线L1、L2相互平行,且都与AB边所在的直线成60°角,设P点运动的时间为x秒(1<x<8),直线L1、L2在菱形ABCD上截得的图形面积为y平方厘米.
如图,菱形ABCD中,∠A=60°,边长为4厘米,动点P从A出发,以1厘米/秒的速度沿A-B-C运动,在P出发1秒后,点Q以同样的速度沿相同的路线运动,过点P、Q的直线L1、L2相互平行,且都与AB边所在的直线成60°角,设P点运动的时间为x秒(1<x<8),直线L1、L2在菱形ABCD上截得的图形面积为y平方厘米.分析 (1)阴影部分的图形不一定总是梯形;有三种情况:①当1<x≤4时;②当4<x<5时;③当5≤x<8时;容易得出结论;
(2)分三种情况:①当1<x≤4时,由等边三角形的性质和梯形面积公式即可得出结果;
②当4<x<5时,连接BD,证出△ABD和△BCD是等边三角形,得出BD=AB=4,由等边三角形的性质和图象面积公式即可得出结果;
③当5≤x<8时,同①得出结果;
(3)当1<x≤4时,由一次函数的性质得出y最大=$\frac{7\sqrt{3}}{4}$;
当4<x<5时,由二次函数的顶点是得出当x=$\frac{9}{2}$时,y最大=$\frac{15\sqrt{3}}{8}$;
当5≤x<8时,由一次函数的性质得出当x=5时,y最大=$\frac{7\sqrt{3}}{4}$;进行比较即可.
解答 解:(1)阴影部分的图形不一定总是梯形;有三种情况:
①当1<x≤4时,阴影部分的图形是梯形;
②当4<xxy5时,阴影部分的图形不是梯形;当
③5≤x<8时,阴影部分的图形是梯形;
(2)分三种情况:
①当1<x≤4时,y=$\frac{1}{2}$(x-1+x)×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$x-$\frac{\sqrt{3}}{4}$;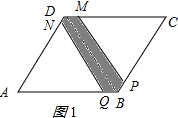
②当4<x<5时,连接BD,如图1所示:
∵四边形ABCD是菱形,∠A=60°,
∴AB=BC=CD=DA=4,
∴△ABD和△BCD是等边三角形,
∴BD=AB=4,y=$\frac{1}{2}$(x-1+4)×$\frac{\sqrt{3}}{2}$(5-x)+$\frac{1}{2}$(4+8-x)×$\frac{\sqrt{3}}{2}$(x-4)=-$\frac{\sqrt{3}}{2}$x2+$\frac{9\sqrt{3}}{2}$x-$\frac{33\sqrt{3}}{4}$;
③当5≤x<8时,如图2所示
y=$\frac{1}{2}$(8-x+9-x)×$\frac{\sqrt{3}}{2}$=-$\frac{\sqrt{3}}{2}$x+$\frac{17}{4}$;
(3)当1<x≤4时,y=$\frac{\sqrt{3}}{2}$x-$\frac{\sqrt{3}}{4}$,y随x的增大而增大,
当x=4时,y最大=$\frac{7\sqrt{3}}{4}$;
当4<x<5时,y=-$\frac{\sqrt{3}}{2}$x2+$\frac{9\sqrt{3}}{2}$x-$\frac{33\sqrt{3}}{4}$=-$\frac{\sqrt{3}}{2}$(x-$\frac{9}{2}$)2+$\frac{15\sqrt{3}}{8}$,
∴当x=$\frac{9}{2}$时,y最大=$\frac{15\sqrt{3}}{8}$;
当5≤x<8时,y=-$\frac{\sqrt{3}}{2}$x+$\frac{17}{4}$$\sqrt{3}$,y随x的增大而减小,
∴当x=5时,y最大=$\frac{7\sqrt{3}}{4}$;
综上所述:∵$\frac{15\sqrt{3}}{8}$>$\frac{7\sqrt{3}}{4}$,
∴当x=$\frac{9}{2}$时,y的值最大,最大值为$\frac{15\sqrt{3}}{8}$.
点评 本题是四边形综合题目,考查了菱形的性质、等边三角形的判定与性质、等边三角形和梯形面积的计算等知识;本题综合性强,有一定难度,需要进行分类讨论才能得出结果.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 阅读材料:
阅读材料:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知正方形ABCD,E是CB延长线上一点,连接DE,交AB于点F,过点B作BG⊥DE于点G,连接AG.
如图,已知正方形ABCD,E是CB延长线上一点,连接DE,交AB于点F,过点B作BG⊥DE于点G,连接AG.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在猜一商品价格的游戏中,参与者事先不知道该商品的价格,主持人要求他从如图的五张卡片中任意拿走三张,使剩下的卡片从左到右连成一个两位数,该数就是他猜的价格.如果商品的价格是50元,那么他一次就能猜中的概率是$\frac{1}{5}$.
在猜一商品价格的游戏中,参与者事先不知道该商品的价格,主持人要求他从如图的五张卡片中任意拿走三张,使剩下的卡片从左到右连成一个两位数,该数就是他猜的价格.如果商品的价格是50元,那么他一次就能猜中的概率是$\frac{1}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
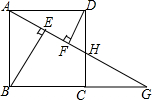 如图,四边形ABCD是正方形,G是BC的延长线上一点,连接AG交CD于点H,BE⊥AG于点E,DF⊥AG于点F.
如图,四边形ABCD是正方形,G是BC的延长线上一点,连接AG交CD于点H,BE⊥AG于点E,DF⊥AG于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com