
 ��ͼ���Ե�P��-1��0��ΪԲ�ĵ�Բ����x����B��C���㣨B��C����ࣩ����y����A��D���㣨A��D���·�����AD=2������ABC�Ƶ�P��ת180�㣬�õ���MCB��
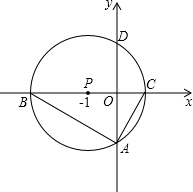
��ͼ���Ե�P��-1��0��ΪԲ�ĵ�Բ����x����B��C���㣨B��C����ࣩ����y����A��D���㣨A��D���·�����AD=2������ABC�Ƶ�P��ת180�㣬�õ���MCB������ ��1������PA�����ô������������ɶ����������Բ�İ뾶���Ӷ��������B��C��������꣮
��2������ԲP�����ĶԳ�ͼ�Σ���Ȼ����AP��ԲP�Ľ���������軭�ĵ�M������MB��MC���ɣ���֤�ı���ACMB�Ǿ��Σ�����M��MH��BC������ΪH����֤��MHP�ա�AOP���Ӷ����MH��OH�ij��������õ���M�����꣮
��3����֤��E��M��B��G���Ե�QΪԲ�ģ�QBΪ�뾶��Բ�ϣ��Ӷ��õ���MQG=2��MBG���ɵ���ֱ�������κ͵��������ε����ʵó���PCA=67.5�㣬�Ӷ��õ���MBG=67.5�㣬�����õ���MQG=135�㣬����MQG�Ķ����Ƕ�ֵ��
��� �⣺��1������PA����ͼ1��ʾ��
��PO��AD��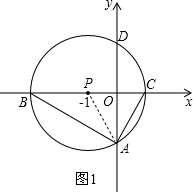
��AO=DO��
��AD=2��
��OA=1��
�ߵ�P����Ϊ��-1��0����
��OP=1��
��PA=$\sqrt{O{P}^{2}+O{A}^{2}}$=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$��
��BP=CP=$\sqrt{2}$��
��OB=$\sqrt{2}$+1��OC=$\sqrt{2}$-1��
��B��-$\sqrt{2}$-1��0����C��$\sqrt{2}$-1��0����
��2������AP���ӳ�AP����P�ڵ�M������MB��MC��
��ͼ2��ʾ���߶�MB��MC��Ϊ��������
�ı���ACMB�Ǿ��Σ��������£�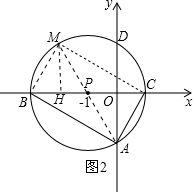
�ߡ�MCB�ɡ�ABC�Ƶ�P��ת180�����ã�
���ı���ACMB��ƽ���ı��Σ�
��BC�ǡ�P��ֱ����
���CAB=90�㣮
��ƽ���ı���ACMB�Ǿ��Σ�
����M��MH��BC������ΪH����ͼ2��ʾ��
�ڡ�MHP�͡�AOP�У�$\left\{\begin{array}{l}{��MHP=��AOP}&{\;}\\{��HPM=��OPA}&{\;}\\{PM=PM}&{\;}\end{array}\right.$��
���MHP�ա�AOP��AAS����
��MH=OA=1��PH=PO=1��
��OH=2��
���M��������-2��1����
��3������ת�����С�MQG�Ĵ�С���䣮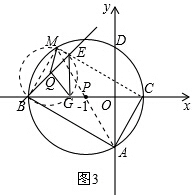
���ı���ACMB�Ǿ��Σ�
���BMC=90�㣮
��EG��BO��
���BGE=90�㣮
���BMC=��BGE=90�㣮
�ߵ�Q��BE���е㣬
��QM=QE=QB=QG��
���E��M��B��G���Ե�QΪԲ�ģ�QBΪ�뾶��Բ�ϣ���ͼ3��ʾ��
���MQG=2��MBG��
��OA=OP=1����AOP=90�㣬
���APC=45�㣬
��PC=PA��
���PCA=��PAC=$\frac{1}{2}$��180��-45�㣩=67.5�㣬
���MBC=��BCA=67.5�㣮
���MQG=135�㣮
������ת�����С�MQG�Ĵ�С���䣬ʼ�յ���135�㣮
���� ���⿼���˴������������ɶ�����ȫ�������ε��ж������ʡ����ε��ж������ʡ�Բ�ܽǶ��������������ε����ʡ��������ڽǺͶ������ĵ㹲Բ��ͼ�ε���ת��֪ʶ���ۺ��ԱȽ�ǿ����һ���Ѷȣ�֤����E��M��B��G���Ե�QΪԲ�ģ�QBΪ�뾶��Բ���ǽ������С��Ĺؼ���


 ȫ�ſ��䵥Ԫ�����������ܸ�ϰϵ�д�
ȫ�ſ��䵥Ԫ�����������ܸ�ϰϵ�д� Ʒѧ˫�ž�ϵ�д�
Ʒѧ˫�ž�ϵ�д� Сѧ��ĩ���100��ϵ�д�
Сѧ��ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��A��B�����������ϱ�ʾ�����ֱ�Ϊa��b������ʽ�ӳ������ǣ�������
��ͼ��A��B�����������ϱ�ʾ�����ֱ�Ϊa��b������ʽ�ӳ������ǣ�������| A�� | a-b��0 | B�� | a+b��0 | C�� | -a+b��0 | D�� | -a-b��0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ABC�У���BAC=70�㣬BC=12��AB����ֱƽ���߽�BC���ڵ�E����AB�ڵ�D��AC�Ĵ�ֱƽ���߽�BC���ڵ�N����AC����M����
��ABC�У���BAC=70�㣬BC=12��AB����ֱƽ���߽�BC���ڵ�E����AB�ڵ�D��AC�Ĵ�ֱƽ���߽�BC���ڵ�N����AC����M�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
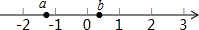 ��֪a��b�������ϵ�λ����ͼ����a+b��a-b��b-a��-a-b�У�����������һ����
��֪a��b�������ϵ�λ����ͼ����a+b��a-b��b-a��-a-b�У�����������һ�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
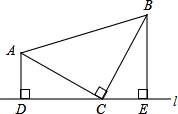 ��ͼ������ֱ��������ABC�У���ACB=90�㣬ֱ��l������C����A��B����ֱ��l��ͬ�ࣩ��AD��l��BE��l������ֱ�ΪD��E����֤����ADC�ա�CEB��
��ͼ������ֱ��������ABC�У���ACB=90�㣬ֱ��l������C����A��B����ֱ��l��ͬ�ࣩ��AD��l��BE��l������ֱ�ΪD��E����֤����ADC�ա�CEB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a+b+c=0 | B�� | a-b+c=0 | C�� | -a-b+c=0 | D�� | -a+b+c=0 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com