
分析 (1)直接利用特殊角的三角函数值将已知数据代入求出答案;
(2)直接利用特殊角的三角函数值将已知数据代入求出答案.
解答 解:(1)$\frac{1}{2}$cos60°+$\frac{\sqrt{3}}{2}$sin60°
=$\frac{1}{2}$×$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$×$\frac{\sqrt{3}}{2}$
=$\frac{1}{4}$+$\frac{3}{4}$
=1;
(2)$\frac{sin60°}{tan45°-cos60°}$
=$\frac{\frac{\sqrt{3}}{2}}{1-\frac{1}{2}}$
=$\sqrt{3}$.
点评 此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
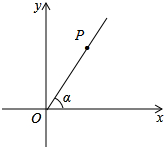 如图,点P是∠α的边OA上的一点,已知点P的横坐标为6,若sinα=$\frac{4}{5}$
如图,点P是∠α的边OA上的一点,已知点P的横坐标为6,若sinα=$\frac{4}{5}$查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
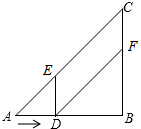 如图,在Rt△ABC中,∠ABC=90°,AB=BC=12cm,点D从点A出发沿AB以2cm/s的速度向B移动,移动过程中始终保持DE∥BC,DF∥AC(点E、F分别在AC、BC上)设运动时间为t s.
如图,在Rt△ABC中,∠ABC=90°,AB=BC=12cm,点D从点A出发沿AB以2cm/s的速度向B移动,移动过程中始终保持DE∥BC,DF∥AC(点E、F分别在AC、BC上)设运动时间为t s.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
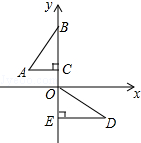 如图,在平面直角坐标系中,点B、C、E、在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,2),AC=4,则这种变换可以是( )
如图,在平面直角坐标系中,点B、C、E、在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,2),AC=4,则这种变换可以是( )| A. | △ABC绕点C逆时针旋转90°,再向下平移2 | |
| B. | △ABC绕点C顺时针旋转90°,再向下平移2 | |
| C. | △ABC绕点C顺时针旋转90°,再向下平移6 | |
| D. | △ABC绕点C逆时针旋转90°,再向下平移6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com