
| A. | (3,-2) | B. | (0,$\frac{3}{2}$) | C. | (3,0) | D. | ($\frac{3}{2}$,0) |
分析 把点的坐标代入函数解析式,看看两边是否相等即可.
解答 解:A、把(3,-2)代入y=3-2x,左边≠右边,
∴点(3,-2)不在函数y=3-2x上,故本选项不符合题意;
B、把(0,$\frac{3}{2}$)代入y=3-2x,左边≠右边,
∴点(0,$\frac{3}{2}$)不在函数y=3-2x上,故本选项不符合题意;
C、把(3,0)代入y=3-2x,左边≠右边,
∴点(3,0)不在函数y=3-2x上,故本选项不符合题意;
D、把($\frac{3}{2}$,0)代入y=3-2x,左边=右边,
∴点($\frac{3}{2}$,0)在函数y=3-2x上,故本选项符合题意;
故选D.
点评 本题考查了一次函数图象上点的坐标特征,能理解函数图象上点的特点是解此题的关键.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:选择题
| A. | 能用完全平方公式,结果是-a2-2ab-b2 | |
| B. | 能用完全平方公式,结果是a2-2ab+b2 | |
| C. | 能用完全平方公式,结果是a2+2ab+b2 | |
| D. | 能用平方差公式,结果是a2-b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
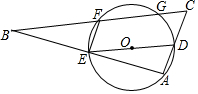 如图,已知ED为⊙O的直径且ED=4,点A(不与E、D重合)为⊙O上一个动点,线段AB经过点E,且EA=EB,F为⊙O上一点,∠FEB=90°,BF的延长线交AD的延长线交于点C.
如图,已知ED为⊙O的直径且ED=4,点A(不与E、D重合)为⊙O上一个动点,线段AB经过点E,且EA=EB,F为⊙O上一点,∠FEB=90°,BF的延长线交AD的延长线交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | -4 | C. | $\frac{3}{4}$ | D. | -$\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在四边形ABCD中,AD∥BC,∠A=90°,AB=12,BC=21,AD=16.动点P从点B出发,沿射线BC的方向以每秒2个单位长的速度运动,动点Q同时从点A出发,在线段AD上以每秒1个单位长的速度向点D运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为t(秒).
如图所示,在四边形ABCD中,AD∥BC,∠A=90°,AB=12,BC=21,AD=16.动点P从点B出发,沿射线BC的方向以每秒2个单位长的速度运动,动点Q同时从点A出发,在线段AD上以每秒1个单位长的速度向点D运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为t(秒).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
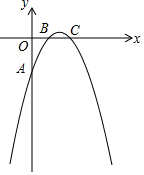 已知二次函数y=-x2+ax+b的图象与y轴交于点A(0,-2),与x轴交于点B(1,0)和点C,D(m,0)(m>2)是x轴上一点.
已知二次函数y=-x2+ax+b的图象与y轴交于点A(0,-2),与x轴交于点B(1,0)和点C,D(m,0)(m>2)是x轴上一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com