
| 抽取柑橘总质量n千克 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 |
| 损坏柑橘质量m千克 | 5.50 | 10.50 | 15.15 | 19.42 | 24.25 | 30.93 | 35.32 | 39.94 |
| 柑橘损坏频率m/n | 0.110 | 0.105 | 0.101 | 0.097 | 0.097 | 0.103 | 0.101 | 0.100 |
分析 (1)根据利用频率估计概率得到随实验次数的增多,发芽的频率越来越稳定在0.1左右,由此可估计柑橘的损坏概率为0.1;
(2)根据概率计算出完好柑橘的质量为10000×0.9=9000千克,设每千克柑橘的销售价为x元,然后根据“售价=进价+利润”列方程解答.
解答 解:(1)根据表中的损坏的频率,当实验次数的增多时,柑橘损坏的频率越来越稳定在0.1左右,所以柑橘的损坏概率为0.1.
故答案为:0.1;
(2)根据估计的概率可以知道,在10000千克柑橘中完好柑橘的质量为10000×0.9=9000千克.
设每千克柑橘的销售价为x元,则应有9000x=2×10000+5000,
解得x≈2.78.
答:出售柑橘时每千克大约定价为2.78元可获利润5000元.
点评 本题考查了利用频率估计概率:用到的知识点为:频率=所求情况数与总情况数之比.得到售价的等量关系是解决(2)的关键.


科目:初中数学 来源: 题型:选择题
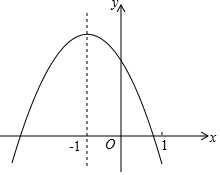 已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中:
已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中:| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com