��1��P��2��-1��
��2����Ϊ��APBΪ����ֱ�������Σ�P������Ϊ��2��-1��
����AB=2��
����A��1��0����B��3��0��
��A�������������y=a��x-2��
2-1�ã�
0=a��1-2��
2-1��
����a=1
���Զ��κ���Ϊ��y=x
2-4x+3
����C��0��3����
����OC=OB����OBC=45��
����Ϊ��ABP=45�㣬
���ԡ�CBD=90�㣬��BCO=45�㣬
���ԡ�BCDΪ����ֱ�������Σ�
����D��0��-3����
��3���ٵ�0��b��3ʱ����ת��ġ�B��C��D�����ACD���ص�����Ϊ��CEM��
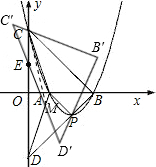
��ΪCE=C��E��
����C��ǡ����ֱ��B��C���ϣ�
CE=3-b��ACֱ�߷���Ϊ��y=3-3x��
E��0��b������EM=
�����ص����֡�CEM�����Ϊ��
S=
����3-b����
=
��0��b��3����
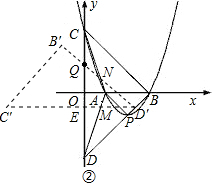
�ڵ�-1��b��0ʱ����ת��ġ�B��C��D�����ACD���ص�����Ϊ�����EMANQ��
��ΪED=ED��=EQ��
����D����ǡ����ֱ��BD�ϣ�DE=EQ=3+b��
����Q��0��3+2b����D�䣨3+b��b����
CQ=3-��3+2b��=-2b��
ACֱ�߷���Ϊ��y=3-3x��
ADֱ�߷���Ϊ��y=3x-3��
D��Qֱ�߷���Ϊ��y=3+2b-x��
����EM=
��N��-b��3+3b��
�����ص����������EMANQ�����Ϊ��
S=S
��ACD-S
��CQN-S
��EMD=
��6��1-
����-2b������-b��-
����3+b����
=
--b+��-1��b��0����
�۵�-3��b��-1ʱ����ת��ġ�B��C��D�����ACD���ص�����Ϊ�ı���EMNQ��
��ΪED=ED��=EQ��
����D���ǡ����ֱ��BD�ϣ�DE=EQ=3+b��
����Q��0��3+2b����D�䣨3+b��b����
DQ=��3+2b��-��-3��=6+2b��
ADֱ�߷���Ϊ��y=3x-3��
D��Qֱ�߷���Ϊ��y=3+2b-x��
����EM=
��N��
��
����
�����ص������ı���EMNQ�����Ϊ��
S=S
��DNQ-S
��EMD=
��(6+2b)��-
��(3+b)��=
��-3��b��1����
�����ص����ֵ����Ϊ��
S= | | (0��b��3) | | --b+(-1��b��0) | | (-3��b��-1) |
| |
��
��0��b��3ʱ��b=0ʱ��S�����S���=
��
��-1��b��0ʱ��S=
--b+=-
-(b+)2+��
b=-
ʱ��S�����S���=
��
��-3��b��-1ʱ��b=-1ʱ��S�����S���=
��
������������b=-
ʱ��S���=
��

 ����y�ύ��ΪC������BP���ӳ���y���ڵ�D��
����y�ύ��ΪC������BP���ӳ���y���ڵ�D��
 �ڵ�-1��b��0ʱ����ת��ġ�B��C��D�����ACD���ص�����Ϊ�����EMANQ��
�ڵ�-1��b��0ʱ����ת��ġ�B��C��D�����ACD���ص�����Ϊ�����EMANQ��

 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�

 �����һ�����㣮
�����һ�����㣮 

 ��A��B�غϣ����ұ���DE��BC����DEΪ�ߣ��ڵ�A�������������DEFG��
��A��B�غϣ����ұ���DE��BC����DEΪ�ߣ��ڵ�A�������������DEFG��