
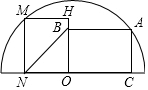
 如图,点M、A在⊙O上,四边形ABOC、MNOH都为矩形,且ON=OB,求证:OH=OC.
如图,点M、A在⊙O上,四边形ABOC、MNOH都为矩形,且ON=OB,求证:OH=OC. 分析 连接OA、OM,利用“HL”证明Rt△AOB和Rt△MON全等,根据全等三角形对应边相等可得MN=AB,根据矩形的对边相等可得MN=OH,AB=OC,等量代换即可得证.
解答  证明:如图,连接OA、OM,
证明:如图,连接OA、OM,
∵点M、A在⊙O上,
∴OA=OM,
在Rt△AOB和Rt△MON中,$\left\{\begin{array}{l}{OA=OM}\\{ON=OB}\end{array}\right.$,
∴Rt△AOB≌Rt△MON(HL),
∴MN=AB,
∵四边形ABOC、MNOH都为矩形,
∴MN=OH,AB=OC,
∴OH=OC.
点评 本题考查了矩形的性质,全等三角形的判定与性质,主要利用了矩形的对边相等,全等三角形对应边相等,作辅助线构造出全等三角形是解题的关键.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:解答题
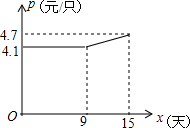 某企业接到一批月饼生产任务,按要求在15天内完成,约定这批月饼的出厂价为每块6元,为按时完成任务,该企业招收了新工人.设新工人王红第x天生产的月饼数量为y块,y与x满足下列关系式:y=$\left\{\begin{array}{l}{54x(0≤x≤5)}\\{30x+120(5≤x≤15)}\end{array}\right.$.
某企业接到一批月饼生产任务,按要求在15天内完成,约定这批月饼的出厂价为每块6元,为按时完成任务,该企业招收了新工人.设新工人王红第x天生产的月饼数量为y块,y与x满足下列关系式:y=$\left\{\begin{array}{l}{54x(0≤x≤5)}\\{30x+120(5≤x≤15)}\end{array}\right.$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com