
 利用图形来表示数量或数量关系,也可以利用数量或数量关系来描述图形特征或图形之间的关系,这种思想方法称为数形结合.我们刚学过的第9章《整式乘法与因式分解》就很好地体现了这一思想方法,你能利用数形结合的思想解决下列问题吗?
利用图形来表示数量或数量关系,也可以利用数量或数量关系来描述图形特征或图形之间的关系,这种思想方法称为数形结合.我们刚学过的第9章《整式乘法与因式分解》就很好地体现了这一思想方法,你能利用数形结合的思想解决下列问题吗?分析 (1)根据题意找出规律进行计算即可;
(2)①根据同底数幂的乘法进行计算即可;
②根据题意画出图形,依次取正方形面积的$\frac{2}{3}$,$\frac{2}{9}$,$\frac{2}{27}$…找出规律即可;
③根据题意画出图形,依次取正方形面积的$\frac{1}{3}$,$\frac{2}{9}$,$\frac{4}{27}$…找出规律即可.
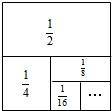
解答 解:(1)∵第一次取走$\frac{1}{2}$后还剩$\frac{1}{2}$,即$\frac{1}{2}$=1-$\frac{1}{2}$;
前两次取走$\frac{1}{2}$+$\frac{1}{4}$后还剩$\frac{1}{4}$,即$\frac{1}{2}$+$\frac{1}{4}$=1-$\frac{1}{4}$;
前三次取走$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$后还剩$\frac{1}{8}$,即$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$=1-$\frac{1}{8}$;
…前 n次取走后还剩下1-$\frac{1}{{2}^{n}}$,
n次取走后还剩下1-$\frac{1}{{2}^{n}}$,
∴$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+$\frac{1}{16}$+…+$\frac{1}{2^n}$=1-$\frac{1}{{2}^{n}}$,
故答案为:1-$\frac{1}{{2}^{n}}$;
(2)①2-22-23-24-25-26-…-22008+22009=2-22009($\frac{1}{{2}^{2007}}$+$\frac{1}{{2}^{2006}}$+…+$\frac{1}{2}$)+22009=2-22009(1-$\frac{1}{{2}^{2007}}$)+22009=2-22009+4+22009=6;
故答案为:6;
②如图所示: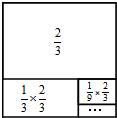
由图可知,$\frac{2}{3}$+$\frac{2}{9}$+$\frac{2}{27}$+…+$\frac{2}{{3}^{n}}$=1-$\frac{1}{{3}^{n}}$.
故答案为:1-$\frac{1}{{3}^{n}}$;
③如图是一个边长为1的正方形,根据图示
由图可知,$\frac{1}{3}$+$\frac{2}{9}$+$\frac{4}{27}$+…+$\frac{{2}^{n-1}}{{3}^{n}}$=1-$\frac{{2}^{n}}{{3}^{n}}$,
故答案为:1-$\frac{{2}^{n}}{{3}^{n}}$.
点评 本题考查的图形的变化类及整式的加减,根据题意画出图形,利用数形结合求解是解答此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
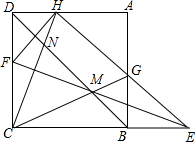 如图,已知正方形纸片ABCD,E为CB延长线上一点,F为边CD上一点,将纸片沿EF翻折,点C恰好落在AD边上的点H,连接BD,CH,CG.CH交BD于点N,EF、CG、BD恰好交于一点M.若DH=2,BG=3,则线段MN的长度为$\frac{5\sqrt{2}}{2}$.
如图,已知正方形纸片ABCD,E为CB延长线上一点,F为边CD上一点,将纸片沿EF翻折,点C恰好落在AD边上的点H,连接BD,CH,CG.CH交BD于点N,EF、CG、BD恰好交于一点M.若DH=2,BG=3,则线段MN的长度为$\frac{5\sqrt{2}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{x+y}$ | B. | $\frac{2}{x+y}$ | C. | $\frac{x+y}{xy}$ | D. | y+x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com