
【题目】如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
(1)求证:四边形EFDG是菱形;
(2)求证:EG2= ![]() AFGF;
AFGF;
(3)若AG=6,EG=2 ![]() ,求BE的长.
,求BE的长.
【答案】
(1)证明:∵GE∥DF,
∴∠EGF=∠DFG.
∵由翻折的性质可知:GD=GE,DF=EF,∠DGF=∠EGF,
∴∠DGF=∠DFG.
∴GD=DF.
∴DG=GE=DF=EF.
∴四边形EFDG为菱形
(2)证明:如图1所示:连接DE,交AF于点O.
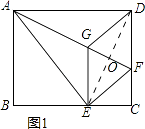
∵四边形EFDG为菱形,
∴GF⊥DE,OG=OF= ![]() GF.
GF.
∵∠DOF=∠ADF=90°,∠OFD=∠DFA,
∴△DOF∽△ADF.
∴ ![]() =
= ![]() ,即DF2=FOAF.
,即DF2=FOAF.
∵FO= ![]() GF,DF=EG,
GF,DF=EG,
∴EG2= ![]() GFAF
GFAF
(3)如图2所示:过点G作GH⊥DC,垂足为H.
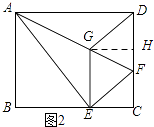
∵EG2= ![]() GFAF,AG=6,EG=2
GFAF,AG=6,EG=2 ![]() ,
,
∴20= ![]() FG(FG+6),整理得:FG2+6FG﹣40=0.
FG(FG+6),整理得:FG2+6FG﹣40=0.
解得:FG=4,FG=﹣10(舍去).
∵DF=GE=2 ![]() ,AF=10,
,AF=10,
∴AD= ![]() =4
=4 ![]() .
.
∵GH⊥DC,AD⊥DC,
∴GH∥AD.
∴△FGH∽△FAD.
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() .
.
∴GH= ![]() .
.
∴BE=AD﹣GH=4 ![]() ﹣
﹣ ![]() =
= ![]()
【解析】(1)先依据翻折的性质和平行线的性质证明∠DGF=∠DFG,从而得到GD=DF,接下来依据翻折的性质可证明DG=GE=DF=EF即可得到四边形EFDG为菱形;
(2)连接DE,交AF于点O.由菱形的性质可知GF⊥DE,OG=OF=![]() GF,接下来,由△DOF∽△ADF,根据相似三角形的性质可证明DF2=FOAF,于是可得到EG2=
GF,接下来,由△DOF∽△ADF,根据相似三角形的性质可证明DF2=FOAF,于是可得到EG2= ![]() GFAF;
GFAF;
(3)过点G作GH⊥DC,垂足为H.利用(2)的结论可求得FG=4,然后再△ADF中依据勾股定理可求得AD的长,然后再证明△FGH∽△FAD,利用相似三角形的性质可求得GH的长,最后依据BE=AD-GH求解即可BE的长.
【考点精析】认真审题,首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2),还要掌握矩形的性质(矩形的四个角都是直角,矩形的对角线相等)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】某中学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进的图书,调查发现,若购买一个乙种书柜比购买一个甲种书柜贵60元,若购买甲种书柜1个、乙种书柜2个,共需资金660元.
(1)甲、乙两种书柜每个的价格分别是多少元?
(2)若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请问学校有哪几种购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B,C三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如表和图一:
A | B | C | |
笔试 | 85 | 95 | 90 |
口试 | 80 | 85 |

(1)请将表一和图一中的空缺部分补充完整.
(2)竞选的最后一个程序是由本系的300名学生进行投票,三位候选人的得票情况如图二(没有弃权票,每名学生只能推荐一个),请计算每人的得票数.
(3)若每票计1分,系里将笔试、口试、得票三项测试得分按4:3:3的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y= ![]() (k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n,
(k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n, ![]() ),过点E的直线l交x轴于点F,交y轴于点G(0,﹣2),则点F的坐标是 .
),过点E的直线l交x轴于点F,交y轴于点G(0,﹣2),则点F的坐标是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批发市场对外批发某品脾的玩具,其价格与件数关系如图所示,请你根据图中描述判断:下列说法中错误的是( )

A. 当件数不超过30件时,每件价格为60元
B. 当件数在30到60之间时,每件价格随件数增加而减少
C. 当件数为50件时,每件价格为55元
D. 当件数不少于60件时,每件价格都是45元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮家与姥姥家相距24km,小亮8:00从家出发,骑自行车去姥姥家![]() 妈妈8:30从家出发,乘车沿相同路线去姥姥家
妈妈8:30从家出发,乘车沿相同路线去姥姥家![]() 在同一直角坐标系中,小亮和妈妈的行进路程与北京时间的函数图象如图所示,根据图象得到如下结论,其中错误的是
在同一直角坐标系中,小亮和妈妈的行进路程与北京时间的函数图象如图所示,根据图象得到如下结论,其中错误的是![]()
![]()

A. 9:00妈妈追上小亮B. 妈妈比小亮提前到达姥姥家
C. 小亮骑自行车的平均速度是![]() D. 妈妈在距家13km处追上小亮
D. 妈妈在距家13km处追上小亮
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是△ABC外接圆⊙O的直径,D是AB延长线上一点,且BD= ![]() AB,∠A=30°,CE⊥AB于E,过C的直径交⊙O于点F,连接CD、BF、EF.
AB,∠A=30°,CE⊥AB于E,过C的直径交⊙O于点F,连接CD、BF、EF.
(1)求证:CD是⊙O的切线;
(2)求:tan∠BFE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】锐锐参加我市电视台组织的“牡丹杯”智力竞答节目,答对最后两道单选题就顺利通关,第一道单选题有3个选项,第二道单选题有4个选项,这两道题锐锐都不会,不过锐锐还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
(1)如果锐锐两次“求助”都在第一道题中使用,那么锐锐通关的概率是 .
(2)如果锐锐两次“求助”都在第二道题中使用,那么锐锐通关的概率是 .
(3)如果锐锐将每道题各用一次“求助”,请用树状图或者列表来分析他顺利通关的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com