
【题目】小敏参加答题游戏,答对最后两道单选题就顺利通关.第一道单选题有3个选项![]() ,
,![]() ,
,![]() ,第二道单选题有4个选项
,第二道单选题有4个选项![]() ,
,![]() ,
,![]() ,
,![]() ,这两道题小敏都不会,不过小敏还有一个“求助”机会,使用“求助”可以去掉其中一道题的一个错误选项.假设第一道题的正确选项是
,这两道题小敏都不会,不过小敏还有一个“求助”机会,使用“求助”可以去掉其中一道题的一个错误选项.假设第一道题的正确选项是![]() ,第二道题的正确选项是
,第二道题的正确选项是![]() ,解答下列问题:
,解答下列问题:
(1)如果小敏第一道题不使用“求助”,那么她答对第一道题的概率是________;
(2)如果小敏将“求助”留在第二道题使用,用画树状图或列表的方法,求小敏顺利通关的概率;
(3)小敏选第________道题(选“一”或“二”)使用“求助”,顺利通关的可能性更大.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)一.
;(3)一.
【解析】
(1)直接利用概率公式求解;
(2)画树状图(用Z表示正确选项,C表示错误选项)展示所有9种等可能的结果数,找出小敏顺利通关的结果数,然后根据概率公式计算出小敏顺利通关的概率;
(3)与(2)方法一样求出小颖将“求助”留在第一道题使用,小敏顺利通关的概率,然后比较两个概率的大小可判断小敏在答第几道题时使用“求助”.
解:(1)若小敏第一道题不使用“求助”,那么小敏答对第一道题的概率=![]() ;
;
故答案为![]() ;
;
(2)若小敏将“求助”留在第二道题使用,那么小敏顺利通关的概率是![]() .理由如下:
.理由如下:
画树状图为:(用Z表示正确选项,C表示错误选项)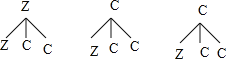
共有9种等可能的结果数,其中小颖顺利通关的结果数为1,
所以小敏顺利通关的概率=![]() ;
;
(3)若小敏将“求助”留在第一道题使用,画树状图为:(用Z表示正确选项,C表示错误选项)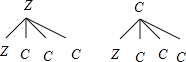
共有8种等可能的结果数,其中小敏顺利通关的结果数为1,所以小敏将“求助”留在第一道题使用,小敏顺利通关的概率=![]() ,
,
由于![]() >
>![]() ,
,
所以建议小敏在答第一道题时使用“求助”.


科目:初中数学 来源: 题型:
【题目】已知如图1,在△ABC中,∠ACB=90°,BC=AC,点D在AB上,DE⊥AB交BC于E,点F是AE的中点
(1)写出线段FD与线段FC的关系并证明;
(2)如图2,将△BDE绕点B逆时针旋转α(0°<α<90°),其它条件不变,线段FD与线段FC的关系是否变化,写出你的结论并证明;
(3)将△BDE绕点B逆时针旋转一周,如果BC=4,BE=2![]() ,直接写出线段BF的范围.
,直接写出线段BF的范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】骆驼被称为“沙漠之舟”,它的体温随时间的变化而发生较大变化,其体温(![]() )与时间(小时)之间的关系如图1所示.
)与时间(小时)之间的关系如图1所示.

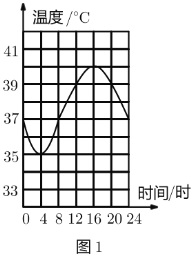
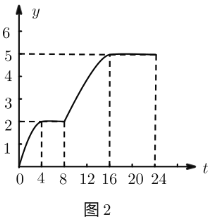
小清同学根据图1绘制了图2,则图2中的变量有可能表示的是( ).
A.骆驼在![]() 时刻的体温与0时体温的绝对差(即差的绝对值)
时刻的体温与0时体温的绝对差(即差的绝对值)
B.骆驼从0时到![]() 时刻之间的最高体温与当日最低体温的差
时刻之间的最高体温与当日最低体温的差
C.骆驼在![]() 时刻的体温与当日平均体温的绝对差
时刻的体温与当日平均体温的绝对差
D.骆驼从0时到![]() 时刻之间的体温最大值与最小值的差
时刻之间的体温最大值与最小值的差
查看答案和解析>>
科目:初中数学 来源: 题型:
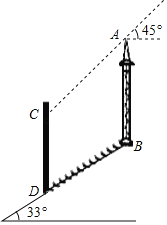
【题目】如图,在坡角为33°的山坡上有一建筑物AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得建筑物AB落在斜坡上的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求建筑物AB的高(AB,CD均与水平面垂直,参考数据:sin33°=0.54,cos33°=0.84,tan33°=0.65)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,对角线
中,对角线![]() ,
,![]() 相交于点
相交于点![]() ,且
,且![]() ,
,![]() .动点
.动点![]() ,
,![]() 分别从点
分别从点![]() ,
,![]() 同时出发,运动速度均为lcm/s.点
同时出发,运动速度均为lcm/s.点![]() 沿
沿![]() 运动,到点
运动,到点![]() 停止.点
停止.点![]() 沿
沿![]() 运动,点
运动,点![]() 到点
到点![]() 停留4
停留4![]() 后继续运动,到点
后继续运动,到点![]() 停止.连接
停止.连接![]() ,
,![]() ,
,![]() ,设
,设![]() 的面积为
的面积为![]() (这里规定:线段是面积为0的三角形),点
(这里规定:线段是面积为0的三角形),点![]() 的运动时间为
的运动时间为![]() .
.
(1)求线段![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(2)求![]() 时,求
时,求![]() 与
与![]() 之间的函数解析式,并写出
之间的函数解析式,并写出![]() 的取值范围;
的取值范围;
(3)当![]() 时,直接写出
时,直接写出![]() 的取值范围.
的取值范围.
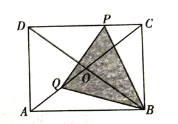
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,(其中
,(其中![]() ),连接
),连接![]() 、
、![]() ,点
,点![]() 为线段
为线段![]() 的中点,连接
的中点,连接![]() 、
、![]() ,
,![]() 绕点
绕点![]() 顺时针旋转,探究线段
顺时针旋转,探究线段![]() 与
与![]() 的数量关系.
的数量关系.
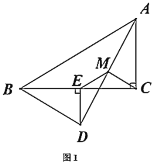
(1)如图1,点![]() 落在
落在![]() 边上时,探究
边上时,探究![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
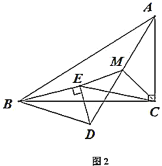
(2)如图2,点![]() 落在
落在![]() 内部时,探究
内部时,探究![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四张卡片,除一面分别写有数字2,2,3,6外,其余均相同,将卡片洗匀后,写有数字的一面朝下扣在桌面上,随机抽取一张卡片记下数字后放回,洗匀后仍将写有数字的一面朝下扣在桌面上,再抽取一张.
(1)用列表或画树状图的方法求两次都恰好抽到2的概率;
(2)小贝和小晶以此为游戏,游戏规则是:第一次抽取的数字作为十位,第二次抽取的数字作为个位,组成一个两位数,若组成的两位数不小于32,小贝获胜,否则小晶获胜.你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王辉在某景区经营一个小摊位,他以10元/根的价格购进一批登山杖,经市场调查发现当售价为24元/根时,每天可出售156根,此后售价每增加5元,就会少售出30根.
(1)求登山杖的单根售价![]() (元)与销售数量
(元)与销售数量![]() (根)之间的函数关系式;
(根)之间的函数关系式;
(2)若设王辉每天的日销售利润为![]() 元,求
元,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)为了避免恶性竞争且保障商家获得一定利润,景区管理处规定登山杖的销售单价不得低于32元且不高于36元,则王辉的日销售利润最大是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究 如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() 两点且与
两点且与![]() 轴的负半轴交于点
轴的负半轴交于点![]() .
.
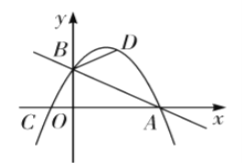
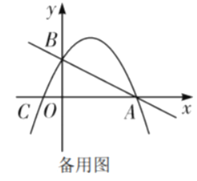
(1)求该抛物线的解析式;
(2)若![]() 为直线
为直线![]() 上方抛物线上的一个动点,当
上方抛物线上的一个动点,当![]() 时,求
时,求![]() 点的坐 标;
点的坐 标;
(3)已知![]() 分别是直线
分别是直线![]() 和抛物线上的动点,当以
和抛物线上的动点,当以![]() 为顶点的四边形 是平行四边形,且以
为顶点的四边形 是平行四边形,且以![]() 为边时,请直接写出所有符合条件的点
为边时,请直接写出所有符合条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com