
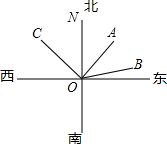
 如图,甲、乙、丙三艘轮船从港口O出发,当分别行驶到A,B,C处时,经测量得,甲船位于港口的北偏东43°45′方向,乙船位于港口的北偏东76°35′方向,丙船位于港口的北偏西43°45′方向.
如图,甲、乙、丙三艘轮船从港口O出发,当分别行驶到A,B,C处时,经测量得,甲船位于港口的北偏东43°45′方向,乙船位于港口的北偏东76°35′方向,丙船位于港口的北偏西43°45′方向.分析 (1)根据方向角的表示方法,可得∠NOA,∠NOB,∠NOC的度数,根据∠BOC=∠NOB+∠NOC可得答案;
(2)根据∠AOB=∠NOB-∠NOA,可得答案.
解答 解:(1)∵甲船位于港口的北偏东43°45′方向,乙船位于港口的北偏东76°35′方向,丙船位于港口的北偏西43°45′方向,
∴∠NOA=43°45′,∠NOB=76°35′,∠NOC=43°45′,
∴∠BOC=∠NOB+∠NOC=76°35′+43°45′=120°20′;
(2)∵∠NOA=43°45′,∠NOB=76°35′,
∴∠AOB=∠NOB-∠NOA=76°35′-43°45′=32°50′.
点评 本题考查了方向角和度分秒的计算,利用方向角的表示方法得出角的大小是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 2个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
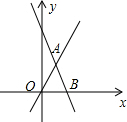 如图:已知直线m:y=2x和直线n:y=kx+10相交于点A,A点横坐标是2.
如图:已知直线m:y=2x和直线n:y=kx+10相交于点A,A点横坐标是2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com