
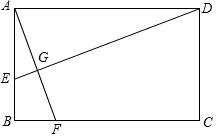
 ��ͼ������ABCD�У�AB=20cm��BC=20$\sqrt{3}$cm������E��AB���ϴӵ�A��ʼ��ÿ��$\sqrt{3}$cm���ٶ����յ�B�˶���ͬʱ������F��BC���ϴӵ�B��ʼ��ÿ��1cm���ٶ����յ�C�˶�����һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶�������DE��AF�ڵ�G��
��ͼ������ABCD�У�AB=20cm��BC=20$\sqrt{3}$cm������E��AB���ϴӵ�A��ʼ��ÿ��$\sqrt{3}$cm���ٶ����յ�B�˶���ͬʱ������F��BC���ϴӵ�B��ʼ��ÿ��1cm���ٶ����յ�C�˶�����һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶�������DE��AF�ڵ�G������ ��1������������Ǻ���ֵ��ȣ��жϳ���BAF=��ADE������ͬ�ǵ���Ǽ��ɵó����ۣ�
��2�����жϳ���G�˶��켣����ADΪֱ����Բ�Ľ�Ϊ60���Բ��������û�����ʽ���ɵó����ۣ�
��3�����жϳ���P����G����̾�����PM��ԲM�ཻʱ��λ�ã�����ù��ɶ������PN���ɣ�
��� �⣺��1�����˶�֪��AE=$\sqrt{3}$t��BF=t��
��Rt��ABF��AB=20��
��tan��BAF=$\frac{BF}{AB}=\frac{t}{20}$��AF=$\sqrt{A{B}^{2}+B{F}^{2}}$=$\sqrt{400+{t}^{2}}$��
��Rt��ADE��AD=20$\sqrt{3}$��
��tan��ADE=$\frac{AE}{AD}=\frac{\sqrt{3}t}{20\sqrt{3}}$=$\frac{t}{20}$��DE=$\sqrt{A{D}^{2}+A{E}^{2}}$=$\sqrt{400��3+3{t}^{2}}$=$\sqrt{3}$��$\sqrt{400+{t}^{2}}$��
��DE=$\sqrt{3}$AF
���BAF=��ADE��
�ߡ�BAF+��DAF=90�㣬
���ADE+��DAF=90�㣬
���AGD=90�㣬
��AF��DE��
����DE=$\sqrt{3}$AF��DE��AF��
��2����ͼ�� ����BD��ȡAD���е�M������BM��
����BD��ȡAD���е�M������BM��
�ɣ�1��֪����AGD=90�㣬
���������˶������У���G���˶��켣����ADΪֱ����Բ�ϵ�һ���֣�
��Rt��ABD��tan��ADB=$\frac{AB}{AD}=\frac{20}{20\sqrt{3}}=\frac{\sqrt{3}}{3}$��
���ADB=30�㣬
���AMB=60�㣬
�ߵ�E�˶�����Bֹͣ��
���G�˶��켣����ADΪֱ����Բ�Ľ�Ϊ60�㣬Բ����
��AM=$\frac{1}{2}$AD=10$\sqrt{3}$��
���G���˶�·����Ϊ$\frac{60�С�10\sqrt{3}}{180}$=$\frac{10\sqrt{3}��}{3}$��
��3����ͼ1��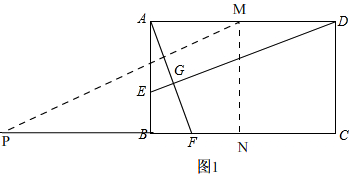 ����PM������M��MN��BC��
����PM������M��MN��BC��
�ߵ�P����G����̾���Ϊ��40-10$\sqrt{3}$����
��PM=40��
��MN=20��
���ݹ��ɶ����ã�PN=$\sqrt{P{M}^{2}-M{N}^{2}}$=20$\sqrt{3}$��
��PB=PN-BN=20$\sqrt{3}$-10$\sqrt{3}$=10$\sqrt{3}$��
���� �������ı����ۺ��⣬��Ҫ�����˾��ε����ʣ����ɶ�����ֱ�������ε����ʣ�������Ǻ������Ȿ��Ĺؼ����жϳ�DE��AF����һ���ѶȲ�����п������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 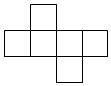 | B�� | 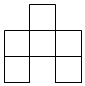 | C�� | 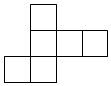 | D�� | 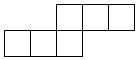 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 65�� | B�� | 50���60�� | C�� | 65���50�� | D�� | 50�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
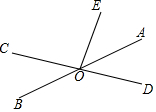 ��֪����ͼ��AB��CD���ڵ�O��OAƽ�֡�EOD����EOD=80�㣮
��֪����ͼ��AB��CD���ڵ�O��OAƽ�֡�EOD����EOD=80�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
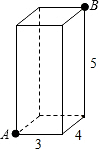 ��ͼ��������ij��������߷ֱ�Ϊ3��4��5��������ϵ�A����B����̾��룮
��ͼ��������ij��������߷ֱ�Ϊ3��4��5��������ϵ�A����B����̾��룮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
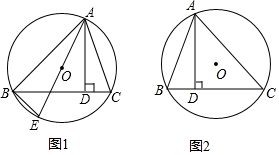 ѧϰ�ˡ�ֱ�����Ե�Բ�ܽ���ֱ�ǡ���һ���ʺ�Բ�н���ֱ��ת���ĵȽǽ�Ϊ���㣬����˵��
ѧϰ�ˡ�ֱ�����Ե�Բ�ܽ���ֱ�ǡ���һ���ʺ�Բ�н���ֱ��ת���ĵȽǽ�Ϊ���㣬����˵���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com