
���� ��1�����������֪�г�ʽ����⣮
��2���Ȼ��������ʽ�ӣ�Ȼ��x��y��ֵ���뼴������𰸣�
��� �⣺��1���������֪��$|\begin{array}{l}{1}&{-2}\\{3}&{-1}\end{array}|$=1����-1��-��-2����3=-1+6=5��
��2���ߣ�x-2��2+��y+$\frac{1}{5}$��2=0��
��x=2��y=-$\frac{1}{5}$��
��$|\begin{array}{l}{-3{x}^{2}+y}&{{x}^{2}+y}\\{3}&{-2}\end{array}|$=-2��-3x2+y��-3��x2+y��
=6x2-2y-3x2-3y
=3x2-5y
=3��4-5����-$\frac{1}{5}$��
=12+1
=13
���� ���⿼���¶��������㣬�漰��ʽ�ļӼ����������������ģ���Ŀ��Ϊ�ۺϣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | xy | B�� | y-x | C�� | 1 | D�� | -1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
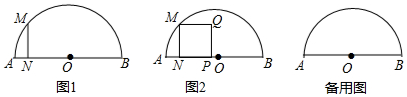
 ��ͼ����֪E��F��������ABCD�ı�BC��CD�ϵ����㣬��AE=AF����ô����AB=4ʱ����AEF�����S��CE�ij�x�ĺ���������ǣ�д�����ı���ʽ�����ش�xȡ��ֵʱ����AEF����������ģ������ʱ��AEF�������������ABCD�����֮�ȣ�
��ͼ����֪E��F��������ABCD�ı�BC��CD�ϵ����㣬��AE=AF����ô����AB=4ʱ����AEF�����S��CE�ij�x�ĺ���������ǣ�д�����ı���ʽ�����ش�xȡ��ֵʱ����AEF����������ģ������ʱ��AEF�������������ABCD�����֮�ȣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
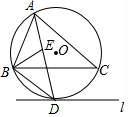 ��ͼ����O�ǡ�ABC�����Բ��ֱ��l���O�����ڵ�D����l��BC��
��ͼ����O�ǡ�ABC�����Բ��ֱ��l���O�����ڵ�D����l��BC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

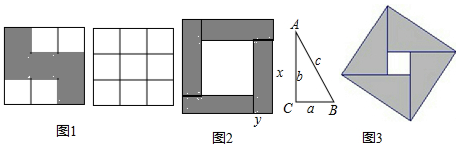
| �����εĸ��� | 1 | 2 | 3 | 4 | �� |
| �����ĸ��� | 3 | 5 | 7 | 9 | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com