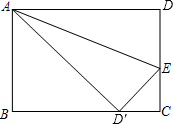
解:∵四边形ABCD为矩形,
∴AD=BC=10cm,DC=AB=6cm,
又∵△AD′E是由△ADE折叠得到,
∴AD′=AD=10cm,D′E=DE,
在Rt△ABD′中,BD′=
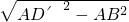
=

=8cm,
∴CD′=2cm,
设CE=xcm,则D′E=DE=(6-x)cm,
在Rt△D′CE中,D′E
2=EC
2+D′C
2,即(6-x)
2=2
2+x
2,
解得x=

,
即CE=

cm.
分析:由四边形ABCD为矩形,AB=6cm,BC=10cm,即可求得AD与AB的长,又由折叠的性质,即可得AD′=AD,然后在Rt△ABD′中,利用勾股定理求得BD′的长,即可得CD′的长,然后设CE=xcm,在Rt△D′CE中,由勾股定理即可得方程:(6-x)
2=2
2+x
2,解此方程即可求得CE的长.
点评:本题考查了折叠的性质,矩形的性质以及勾股定理.此题难度适中,解题的关键是注意数形结合思想与方程思想的应用,注意折叠中的对应关系.

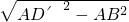 =
= =8cm,
=8cm, ,
, cm.
cm.
