
分析 (1)①先根据跨度的定义先确定出点到圆的最小距离d和最大距离D,即可得出跨度;
②分点在圆内和圆外两种情况同①的方法计算,判定得出结论;
(2)先判断出存在的点P必在圆O内,设出点P的坐标,利用点P到圆心O的距离的2倍是点P到圆的距离跨度,建立方程,由于存在距离跨度是2的点,此方程有解即可得出k的范围.
(3)同(2)方法判断出存在的点P在圆C内部,由于在射线OA上存在距离跨度是2的点,同(2)的方法建立方程,用一元二次方程根与系数的关系和根的判别式即可确定出范围.
解答 解:(1)如图1,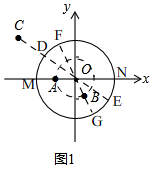
①∵图形G1为以O为圆心,2为半径的圆,∴直径为4,
∵A(-1,0),OA=1,
∴点A到⊙O的最小距离d=MA=OM-OA=1,
点A到⊙O的最大距离D=AN=ON+OM=2+1=3,
∴点A到图形G1的距离跨度R=D-d=3-1=2;
∵B($\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$),∴OB=$\sqrt{(\frac{1}{2})^{2}+(\frac{\sqrt{3}}{2})^{2}}$=1,
∴点B到⊙O的最小距离d=BG=OG-OB=1,
点B到⊙O的最大距离D=BF=FO+OB=2+1=3,
∴点B到图形G1的距离跨度R=D-d=3-1=2;
∵C(-3,2),
∴OC=$\sqrt{(-3)^{2}+{2}^{2}}$=$\sqrt{13}$,
∴点C到⊙O的最小距离d=CD=OC-OD=$\sqrt{13}$-2,
点C到⊙O的最大距离D=CE=OC+OE=2+$\sqrt{13}$
∴点C到图形G1的距离跨度R=D-d=2+$\sqrt{13}$-($\sqrt{13}$-2)=4;
∴圆,
理由:①设⊙O内一点P的坐标为(x,y),
∴OP=$\sqrt{{x}^{2}+{y}^{2}}$,
∴点P到⊙O的最小距离d=2-OP,点P到⊙O的最大距离D=2+OP,
∴点P到图形G1的距离跨度R=D-d=2+OP-(2-OP)=2OP;
∵图形G1的距离跨度为2,
∴2OP=2,
∴OP=1,
∴$\sqrt{{x}^{2}+{y}^{2}}$=1,
∴x2+y2=1,
即:到图形G1的距离跨度为2的所有的点组成的图形的形状是以点O为圆心,1为半径的圆.
②设⊙O外一点Q的坐标为(x,y),
∴OQ=$\sqrt{{x}^{2}+{y}^{2}}$,
∴点Q到⊙O的最小距离d=OQ-2,点P到⊙O的最大距离D=OQ+2,
∴点P到图形G1的距离跨度R=D-d=OQ+2-(OQ-2)=4;
∵图形G1的距离跨度为2,
∴此种情况不存在,
所以,到图形G1的距离跨度为2的所有的点组成的图形的形状是以点O为圆心,1为半径的圆.
故答案为:圆;
(2)设直线y=k(x+1)上存在到G2的距离跨度为2的点P(m,k(m+1)),
∴OP=$\sqrt{(m-1)^{2}+[k(m+1)]^{2}}$,
由(1)②知,圆内一点到图形圆的跨度是此点到圆心距离的2倍,圆外一点到图形圆的跨度是此圆的直径,
∵图形G2为以C(1,0)为圆心,2为半径的圆,到G2的距离跨度为2的点,
∴距离跨度小于图形G2的圆的直径4,
∴点P在图形G2⊙C内部,
∴R=2OP=2$\sqrt{(m-1)^{2}+[k(m+1)]^{2}}$,
∵直线y=k(x+1)上存在到G2的距离跨度为2的点P,
∴2$\sqrt{(m-1)^{2}+[k(m+1)]^{2}}$=2,
∴(k2+1)m2+2(k2-1)m+k2=0①,
∵存在点P,
∴方程①有实数根,
∴△=4(k2-1)2-4×(k2+1)k2=-12k2+4≥0,
∴-$\frac{\sqrt{3}}{3}$≤k≤$\frac{\sqrt{3}}{3}$,
(3)同(2)的方法得出,射线OA上存在点P到圆C的距离跨度为2时,点P在圆内,
设点P(n,$\frac{\sqrt{3}}{3}$n),(n>0),
∵圆心C(x2,0),∴PC=$\sqrt{(n-{x}_{2})^{2}+(\frac{\sqrt{3}}{3}n)^{2}}$=$\frac{1}{2}$×2=1,
∴$\frac{4}{3}$n2-2x2n+x22-1=0,
∴射线OA上存在点到圆C的距离跨度为2,
∴$\left\{\begin{array}{l}{△=4{{x}_{2}}^{2}-4×\frac{4}{3}({{x}_{2}}^{2}-1)≥0}\\{{n}_{1}+{n}_{2}=\frac{2{x}_{2}}{\frac{4}{3}}>0}\\{{n}_{1}{n}_{2}=\frac{{{x}_{2}}^{2}-1}{\frac{4}{3}}>0}\end{array}\right.$,
∴-1≤x2≤2.
点评 此题是圆的综合题,主要考查了新定义,理解和应用新定义解决问题,还涉及到平面坐标系内,两点间的距离公式,一元二次方程的根的判别式,根与系数的关系,由(1)的已知点的坐标计算距离跨度,观察得出规律是解本题的关键.是一道难点比较大的中考常考题,判断出图形的形状是圆,是本题的难点.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2016-2017学年浙江省七年级3月月考数学试卷(解析版) 题型:解答题
如图:在正方形网格中有一个△ABC,按要求进行下列作图(只借助于网格,需写出结论):
(1)过点B画出AC的平行线;
(2)画出先将△ABC向右平移5格,得到△A’B’C’,再向上平移3格后的△A”B”C”;
(3)对于(2)里面这两次平移的得到的图形能通过△ABC一次性平移得到吗?如果可以请你用合适的语言描述这个过程。

查看答案和解析>>
科目:初中数学 来源:2016-2017学年浙江省七年级3月月考数学试卷(解析版) 题型:填空题
如图,直线 ∥
∥ ,∠3+∠4=35°,∠2=90°,则∠1=_______________。
,∠3+∠4=35°,∠2=90°,则∠1=_______________。

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
如图,平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
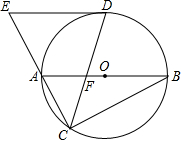 如图,⊙O是△ABC的外接圆,AB为⊙O的直径,∠ACB的平分线交⊙O于点D,交AB于点F;过D作⊙O的切线,交CA延长线于点E.
如图,⊙O是△ABC的外接圆,AB为⊙O的直径,∠ACB的平分线交⊙O于点D,交AB于点F;过D作⊙O的切线,交CA延长线于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 24 cm2 | B. | 48 cm2 | C. | 24π cm2 | D. | 12π cm2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com