
分析 (1)方程的两边同时除以x,通过移项可以得到x+$\frac{1}{x}$的值;
(2)由(1)中的(x+$\frac{1}{x}$)平方后来求x2+$\frac{1}{{x}^{2}}$的值;
(3)x-$\frac{1}{x}$=±$\sqrt{(x+\frac{1}{x})^{2}-4}$.
解答 解:(1)在方程x2-5x+1=0的两边同时除以x,得
x-5+$\frac{1}{x}$=0,
所以x+$\frac{1}{x}$=5;
(2)由(1)知,x+$\frac{1}{x}$=5,
所以(x+$\frac{1}{x}$)2=52,即x2+$\frac{1}{{x}^{2}}$+2=25,
所以x2+$\frac{1}{{x}^{2}}$=23;
(3)∵(x-$\frac{1}{x}$)2=(x+$\frac{1}{x}$)2-4=21,
∴x-$\frac{1}{x}$=±$\sqrt{21}$.
点评 本题考查了一元二次方程的解的定义.熟练掌握完全平方公式以及对完全平方公式的变形公式是解题的关键.


 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:初中数学 来源: 题型:解答题
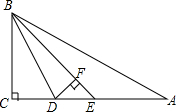 如图,在直角三角形ABC中,∠C=90°,BD是△ABC的角平分线,BE是△BDA的角平分线,DF是△BDE的高线,已知∠DBE=15°,求∠A和∠EDF的度数.
如图,在直角三角形ABC中,∠C=90°,BD是△ABC的角平分线,BE是△BDA的角平分线,DF是△BDE的高线,已知∠DBE=15°,求∠A和∠EDF的度数.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x1=1,x2=3 | B. | x=2±2$\sqrt{3}$ | C. | x=2±$\sqrt{3}$ | D. | x=-2±2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{{2}^{2}+{3}^{2}}$=2+3 | B. | 3$\sqrt{2}$+5$\sqrt{3}$=8$\sqrt{6}$ | ||
| C. | $\sqrt{1{5}^{2}-1{2}^{2}}$=$\sqrt{15+12}$×$\sqrt{15-12}$ | D. | $\sqrt{4\frac{1}{2}}$=2$\sqrt{\frac{1}{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com