
【题目】某商店选用甲、乙两种糖果混合成杂拌糖果后出售,甲的价格为每千克 28 元,乙的价格为每千克 20 元,为使这种杂拌糖果的售价是每千克 25 元,要配置这种杂拌糖果 100 千克,问要用这两种糖果各多少千克?
科目:初中数学 来源: 题型:
【题目】如图,等腰直角三角形ABC,AB=BC,直角顶点B在直线PQ上,且AD⊥PQ于D,CE⊥PQ于E.
(1)△ADB与△BEC全等吗?为什么?
(2)图1中,AD、DE、CE有怎样的等量关系?说明理由.

(3)将直线PQ绕点B旋转到如图2所示的位置,其他条件不变,那么AD,DE,CE有怎样的等量关系?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)观察下列图形与等式的关系,并填空

(2)观察下图,根据(1)中结论,计算图中黑球的个数,用含有n的代数式填空:

1+3+5+…+(2n﹣1)+(______)+(2n﹣1)+…+5+3+1=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年全球葵花籽产量约为4200万吨,比2014年上涨2.1%,某企业加工并销售葵花籽,假设销售量与加工量相等,在图中,线段AB、折线CDB分别表示葵花籽每千克的加工成本y1(元)、销售价y2(元)与产量x(kg)之间的函数关系;
(1)请你解释图中点B的横坐标、纵坐标的实际意义;
(2)求线段AB所表示的y1与x之间的函数解析式;
(3)当0<x≤90时,求该葵花籽的产量为多少时,该企业获得的利润最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
分解因式:x2+2x-3
解:原式=x2+2x+1-1-3
=(x2+2x+1)-4
=(x+1)2-4
=(x+1+2)(x+1-2)
=(x+3)(x-1)
此种方法抓住了二次项和一次项的特点,然后加一项,使这三项成为完全平方式,我们把这种分解因式的方法叫配方法.请仔细体会配方法的特点,然后尝试用配方法解决下列问题:
(1)分解因式:m2-4mn+3n2;
(2)无论m取何值,代数式m2-3m+2015总有一个最小值,请你尝试用配方法求出它的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学组织初一、初二学生举行“四城同创”宣传活动,从学校坐车出发,先上坡到达A地后,宣传8分钟;然后下坡到B地宣传8分钟返回,行程情况如图.若返回时,上、下坡速度保持不变,在A地仍要宣传8分钟,则他们从B地返回学校用的时间是( )
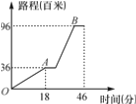
A. 48分钟 B. 45.2分钟 C. 46分钟 D. 33分钟
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com