
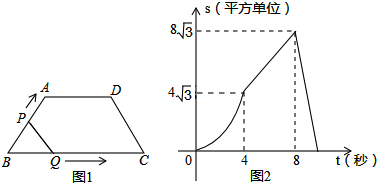
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
���� ���ݵ������ε����ʼ����㺯��ͼ������ʣ��ۺ��жϿɵô𰸣�
��� 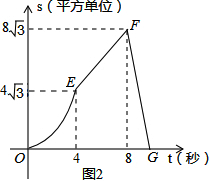 �⣺�ɴ�ͼ2��ʾ�������˶����̷�Ϊ�����Σ�
�⣺�ɴ�ͼ2��ʾ�������˶����̷�Ϊ�����Σ�
��1��OE�Σ�����ͼ��Ϊ�����ߣ��˶�ͼ�����ͼ1-1��ʾ��
��ʱ��P���߶�AB�ϡ���Q���߶�BC���˶���
��BPQΪ�ȱ������Σ���߳�BP=BQ=t����h=$\frac{\sqrt{3}}{2}$t��
��S=$\frac{1}{2}$BQ•h=$\frac{1}{2}$t•$\frac{\sqrt{3}}{2}$t=$\frac{\sqrt{3}}{4}$t2��
�ɺ���ͼ���֪����t=4��ʱ��S=4$\sqrt{3}$����ѡ��A��ȷ��
��2��EF�Σ�����ͼ��Ϊֱ�ߣ��˶�ͼ�����ͼ1-2��ʾ��
��ʱ��P���߶�AD�ϡ���Q���߶�BC���˶���
�ɺ���ͼ���֪���˽��˶�ʱ��Ϊ4s��
��AD=1��4=4����ѡ��B��ȷ��
��ֱ��EF�Ľ���ʽΪ��S=kt+b����E��4��4$\sqrt{3}$����F��8��8$\sqrt{3}$������ã�
$\left\{\begin{array}{l}{4k+b=4\sqrt{3}}\\{8k+b=8\sqrt{3}}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=\sqrt{3}}\\{b=0}\end{array}\right.$��
��S=$\sqrt{3}$t����ѡ��C����
��3��FG�Σ�����ͼ��Ϊֱ�ߣ��˶�ͼ�����ͼ1-3��ʾ��
��ʱ��P��Q�����߶�CD���˶���
�����θ�Ϊh����S����ABCD=$\frac{1}{2}$��AD+BC��•h=$\frac{1}{2}$��4+8��•h=6h��
��t=9sʱ��DP=1����CP=3��
��S��BCP=$\frac{3}{4}$S��BCD=$\frac{3}{4}$��$\frac{1}{2}$��8��h=3h��
��S��BCP=$\frac{1}{2}$S����ABCD����BPƽ������ABCD���������ѡ��D��ȷ��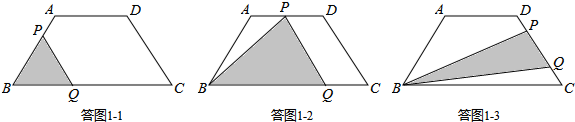
��������������Ľ�����C��
��ѡ��C��
���� ���⿼���˶�������ĺ���ͼ���������һ�����Ѷȣ�����ؼ��ǽ�Ϻ���ͼ���뼸��ͼ�ε�������⣮


 ��ѧʵ����ϵ�д�
��ѧʵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
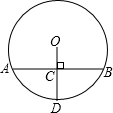 ��ͼ����֪��O�İ뾶OD����AB���ഹֱ������Ϊ��C����AB=16cm��CD=6cm�����O�İ뾶Ϊ��������
��ͼ����֪��O�İ뾶OD����AB���ഹֱ������Ϊ��C����AB=16cm��CD=6cm�����O�İ뾶Ϊ��������| A�� | $\frac{25}{3}$ cm | B�� | 10cm | C�� | 8cm | D�� | $\frac{19}{3}$ cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 8 | B�� | -8 | C�� | 6 | D�� | -6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1��2��3 | B�� | 2��3��4 | C�� | 3��4��5 | D�� | 4��5��6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��� | B�� | ��С | C�� | ���� | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����Rt��ABC�У���ACB=90��AC=3��BC=4���ֱ���AB��AC��BCΪ����ABͬ����������ABEF��ACPQ��BDMC�����Ŀ���Ӱ���ֵ�����ֱ�ΪS1��S2��S3��S4����S1+S2+S3+S4=18��
��ͼ����Rt��ABC�У���ACB=90��AC=3��BC=4���ֱ���AB��AC��BCΪ����ABͬ����������ABEF��ACPQ��BDMC�����Ŀ���Ӱ���ֵ�����ֱ�ΪS1��S2��S3��S4����S1+S2+S3+S4=18���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
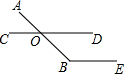 ��ͼ����O�ǡ�ABE�ı�BA�ϵ�һ�㣬����O��ֱ��CD��BE������AOC=40�㣬���B�Ķ���Ϊ��������
��ͼ����O�ǡ�ABE�ı�BA�ϵ�һ�㣬����O��ֱ��CD��BE������AOC=40�㣬���B�Ķ���Ϊ��������| A�� | 160�� | B�� | 140�� | C�� | 60�� | D�� | 50�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
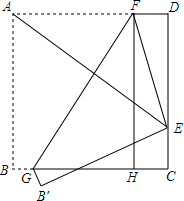 ��ͼ�����߳�Ϊ4��������ABCD�۵���ʹ�õ�A����CD���ϵĵ�E������B���ڵ�B�䴦���ۺ�ΪGF��FH��BC�ڵ�H��FG=5
��ͼ�����߳�Ϊ4��������ABCD�۵���ʹ�õ�A����CD���ϵĵ�E������B���ڵ�B�䴦���ۺ�ΪGF��FH��BC�ڵ�H��FG=5�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com