2012年扬州某学校组织七年级(1)班学生于清明节上午七时乘客车沿淮江高速公路前往距离扬州150千米的淮安楚州“爱国主义教育基地”周恩来纪念馆参观学习,车速是每小时60千米.王老师于半小时后驾驶轿车从扬州出发去追赶客车.问:
(1)若王老师驾驶的轿车车速是每小时80千米,需要多长时间才能追上客车?追上客车时离淮安楚州还有多远?
(2)如果王老师驾驶的轿车要和客车同时到达目的地,那么他驾驶的轿车的速度是多少?
解:(1)设需要x小时才能追上客车,
由题意得,60(x+

)=80x,
解得:x=1.5,
此时客车距离淮安楚州还有:150-80x=30千米;
答:王老师需要1.5小时才能追上客车,追上客车时离淮安楚州还有30千米.
(2)设王老师驾驶的轿车的速度是每小时y千米,
由题意得:
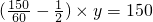
,
解得:y=75,
答:王老师驾驶的轿车的速度是每小时75千米.
分析:(1)设需要x小时才能追上客车,根据追上客车时所走路程相等,可建立方程,得出相遇的时间可求出客车所走的路程,也可求出上客车时离淮安楚州的距离.
(2)根据先计算出客车到达目的地需要的时间,然后可求出轿车到达目的地需要的时间,根据路程=速度×时间,可得出方程,解出即可.
点评:本题考查了一元一次方程的应用,解答本题的关键是读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

 )=80x,
)=80x,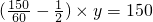 ,
,
